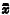 for the negative of x and + for or):
for the negative of x and + for or):
| Peirce page | gnoxic studies |
Charles S. Peirce contributed many definitions to the Dictionary of Philosophy and Psychology edited by J.M. Baldwin (New York: Macmillan, 1902). Items in the list below link to the definitions which are given on this page. These include all entries by Peirce beginning with letters A through O, as previously collected by John Sowa from Christopher D. Green's online version at the Classics in the History of Psychology website. The other entries by Peirce are all in Volume II of Baldwin's Dictionary (Le to Z), which can be viewed at the Internet Archive http://www.archive.org/details/philopsych02balduoft. (Volume 1 is also online.) Some of these other entries are transcribed here, and more will be added as time permits.
Some of the articles included below are co-authored by Peirce, most often with his former student Christine Ladd-Franklin (C.L.F.), or with the Dictionary's general editor James Mark Baldwin (J.M.B.). For a key to all author abbreviations see Vol. 1, p. 7-8, or the York U. site (though this transcription is not entirely error-free).
Many entries in Baldwin's Dictionary not included or listed here will also be of interest to students of Peirce or pragmatism—for instance, the entry on Victoria Welby's Significs (v.II p. 529), and many entries by John Dewey.
| Dualism (in philosophy) [1st para. C.S.P.- A.S.P.P., the rest A.S.P.P.] |
| Economy (logical principle of) | Empirical Logic [1st para. R.A.-C.S.P., the rest R.A.] | Equipollence or -cy [1st para. C.S.P., 2nd para. R.A.] |
| Genus (in logic) | Given | |
|
Imaging (in logic) [C.S.P., H.B.F.] Implicit (in logic) Inconsistency |
Independence Index (in exact logic) Individual (in logic) Inference (in logic) |
Insolubilia Intention (in logic) Involution |
| Kind | Knowledge (in logic) [C.S.P., C.L.F.] | |
|
Laws of Thought [mostly C.S.P, part by C.L.F.] Leading of Proof Leading Principle Lemma |
Light of Nature Limitative Limiting Notion [J.M.B.- C.S.P.] Logic [C.S.P., C.L.F.] |
Logic (exact) Logical Logical Diagram (or Graph) Logomachy |
|
Major and Minor (extreme, term, premise, satz,
&c., in logic) Mark [1st two paras. C.S.P., C.L.F., remaining two paras., C.S.P] Material Fallacy Material Logic Mathematical Logic Matter and Form [contains over 4,050 words] |
Maxim (in logic) Method and Methodology, or Methodeutic Middle Term (and Middle) [C.S.P, C.L.F.] Mixed Mnemonic Verses and Words (in logic) Modality [contains over 2,900 words] |
Modulus Modus ponens and Modus tollens Monad (Monadism, Monadology) [1st para. A.S.P.P.- J.M.B., next four paras. C.S.P., the rest by others] Multitude (in mathematics) [C.S.P, H.B.F.] |
|
Name (in logic) Necessary (in logic) Necessity [by J.D. with list of ‘distinctions’ at end by C.S.P.] Negation [mostly C.S.P., C.L.F.] |
Negative [C.S.P except ‘negative term’ sub-entry which is by C.L.F.] Nominal Nomology Non-A |
Non-Contradiction Non sequitur Norm (and Normality) [1st sentence C.S.P., rest by J.J.] Nota Notae Numerical |
|
Observation [C.S.P., J.M.B.] Obversion |
Opposition (in logic) | Organon |
Peirce's entries listed below, if not given here, can be found in Volume II of Baldwin's Dictionary at the Internet Archive: http://www.archive.org/details/philopsych02balduoft; page numbers are given in brackets to facilitate finding them.
|
P (in logic) Paradox Paralogism [259] Parity [263] Parsimony Partial [265] Particular Particulate Parva Logicalia [266] Per Accidens [276] Perseity (1) and (2) Per se (first two paras. J.D., rest by C.S.P.) [281-2] Perspicuity Pertinent [287, CP 2.602] Petitio Principii (C.S.P., C.L.F.) [287-8] Philosopheme [290] Plurality of Causes Positive Possibility, Impossibility, and Possible (first half J.D., second half C.S.P.) |
Postpredicament [315] Postulate Poly- [309] Port Royal Logic [310] Pragmatic and Pragmatism Precise Precision Predesignate Predicable [325] Predicament Predicate Predication (in logic) Predicative Proposition Premise (and Premiss) Presumption in logic [337] Presumptive Inference: See Probable Inference Presupposition Prime Primum Cognitum Principal [341] |
Priority [342-3] Privation [343] part C.S.P., part J.M.B. Probable Deduction, see Probable Inference Probable Inference Problem Problematic Progressive (in logic) [358] Proof [359] Proposition [361-70] —mostly by C.L.F.-J.M.B.; a sentence on 361-2 says, ‘Cf. the view of proposition given under subject (in logic, 2), which is in certain respects different from what follows. (C.S.P.-J.M.B.)’ Prosyllogism [370] Protasis [371] Provisional [373] Proximate [373-4] Pure (in logic) [401-2, CP 2.544-6] |
| Quality (in grammar and logic) | Quantity (in logic and mathematics) |
|
Ratio [415] Ratiocination [415] Rational (3) In mathematics [415] Reasoning |
Reductio ad absurdum [434, CP 2.612] Reduction [434-5, CP 2.585-7] Regular [438-9, CP 2.601] Relatives (logic of) [447-450; CP 3.636-643] Remote |
Represent [and Representamen] Representationism Repugnance [466] Residues (method of) [467-8] Rule [481] |
|
S (in logic) [483] Saltus [484] Scientific Method (C.S.P., J.M.B.) Scope [503] Secundum quid [504] Series [521] Sign Signification (and Application, in logic) Simple [531-2] —some parts co-authored by J.M.B. Singular Solution [554] Some (in logic) [555] —one sentence (C.L.F., C.S.P.); the rest C.L.F. or J.M.B. Sophism [556] |
Sorites [557] Species (and Specific Marks, in logic) [567] (C.S.P.-J.M.B.) Spurious Proposition [588, CP 2.607] State (and Condition) [593] —1st para. J.M.B., the rest C.S.P. Subalternation [606] Subcontrary [607] Subject (in logic) Sublation [611] Substitution (in logic) [614-15] Subsumption [615] Sufficient Reason [616-17] —mostly C.S.P., some parts C.L.F. and J.M.B. Supposition [624-5] |
Syllogism [628-639, CP 2.552-580] —very long article, with parts by C.L.F. and J.M.B. but most by C.S.P. Symbol Symbolic Logic or Algebra of Logic [640-51, CP 4.372-393] —First part (640-45) and ‘Literature’ list at the end are attributed to (L.C., C.L.F.). Section on Peirce's graphical system (645-50) by C.S.P., with following para. (C.S.P., C.L.F.), = CP 4.372-393. Final paragraph by C.L.F.. Symbolical [651] Synechism Synthetic |
|
Tautology [663] Term Testimony Thema Theorem Theory |
Thesis Transposition (in logic) (C.L.F., C.S.P.) Tree of Porphyry [714, with diagram] Trilemma [715] |
Trivium [716] Truth (and Falsity and Error), Logical Tychism [721] — by (J.D.) but consists mostly of quotations from Peirce. |
|
Ultimate Uniformity |
Unity (and Plurality) |
Universal (and Universality) Universe (the) (C.S.P., C.L.F.) |
|
Vague Validity (C.S.P., C.L.F.) |
Verification |
Virtual |
| Whole (and Parts) |
Note by John Sowa(?): Charles Sanders Peirce contributed several dozen definitions to the Dictionary of Philosophy and Psychology, which was edited by James Mark Baldwin and published by the Macmillan Company in 1901. The following list of definitions by Peirce, many of which are short essays, has been extracted from an online version, which was developed by Christopher D. Green at York University, Toronto.
These definitions may be of interest to philosophers, logicians, and historians for several reasons: they present short summaries of themes that Peirce treated at length in publications; they indicate Peirce's thoughts on other topics that he seldom addressed in his writings; and they show the breadth and depth of Peirce's scholarship. The number of references give some indication: Aristotle is first with 62 references, and Kant is second with 40; others include Schröder 14, Hamilton 13, Hegel 12, Acquinas 11, Leibniz 11, De Morgan 10, Plato 9, Duns Scotus 8, Ockham 5; those with 4 references each include Petrus Hispanus, Boole, Cantor, and Dedekind; many others have one, two, or three references.
The initials C.S.P. mark contributions by Peirce. Some of the definitions were coauthored with other contributors, two of whom were former students of Peirce's at Johns Hopkins University: Christine Ladd-Franklin (C.L.F.) and John Dewey (J.D.). Others include R. Adamson (R.A.), James Mark Baldwin (J.M.B.), H. B. Fine (H.B.F.), E. Morselli (E.M.), and Andrew Seth Peingle-Pattison (A.S.P.P.).
Dualism (in philosophy). (1) A general tendency to divide any genus of objects of philosophical thought into two widely separate categories, as saints and sinners, truth and falsehood, &c.; opposed to the tendency to look for gradations intermediate between contraries. Especially (2) any theory which explains the facts of the universe by referring them to the action of two independent and eternally coexistent principles. Cf. PLURALISM. (C.S.P.- A.S.P.P.)
Economy (logical principle of). A principle maintained by E. Mach that general concepts are merely an adaptation for the economy of mental process. That they have that effect was noticed by Locke. (C.S.P.)
Empirical Logic: Ger. empirische Logik; Fr. logique empirique; Ital. logica empirica. The treatment of logic on the basis or from the point of view of a sensationalist or other markedly empiricist theory of knowledge. (R.A.- C.S.P.)
Equipollence or -cy [Lat. aequus, equal, + pollere, to be able]: Ger. Aequipollenz; Fr. équipollence; Ital. equipollenza. The relation between two propositional forms which represent the same fact. It translates the Gr. ισοδυναμων. (C.S.P.)
Genus (in logic) [Lat. genus, birth]: Ger. Genus; Fr. genre; Ital. genere. A class which contains within its extension, or is divisible into, smaller classes, called relatively species.
The significance of the term has always shared the ambiguity which is discernible in classification. Genera have been distinguished partly by reason of the obvious differences in the larger types of natural forms, partly by reference to the relatively arbitrary process of arranging in accordance with selected marks. The first or empirical factor is predominant in the popular sense of the term, and in much of the Aristotelian and Scholastic logic; the second has been insisted on in the more strictly formal logic. The divergence of the two views makes itself manifest at the limits of classification, at the conception of a summum genus and an infima species, which tend on the one view to be regarded as having a place in rerum natura, while on the other they are but ideal boundaries to an arbitrary process. (R.A.)
One of the Aristotelian rules of DIVISION (q.v.) in logic is that the differences of different genera are different, that is to say, cross-divisions are not to be made. This rule is signally violated in the modern classifications of chemistry, mathematics, and logic itself; but in biology, owing to the common origin of species, the classification is hierarchical, as Aristotle required. Cf. PREDICABLES (C.S.P.)
Given [AS. gifan]: Ger. (das) Gegebene; Fr. (la) donnée; Ital. (il) dato. One of the hypotheses of a problem; used also in the Latin form datum (of which it is a translation). In Greek mathematics, the corresponding word was also extended to whatever is determined in certain specified ways by a given hypothesis. The plural data is loosely applied to any unquestioned knowledge upon which a judgment is based, and in particular to our percepts, in the phrase ‘data of experience.’
The English adjective, given, has an exceedingly convenient use to indicate that that which its noun denotes must be understood as specified (in the verification of what is said) previously to the specification of something mentioned before. Thus, ‘Some woman is adored by any given man,’ is said to avoid all possibility of understanding the statement as ‘Some woman is adored by every man.’ (C.S.P.)
Imaging (in logic): Ger. Abbildung; Fr. (in mathematics) représentation; Ital. rappresentazione. A term proposed to translate Abbildung in its logical use. In order to apprehend this meaning, it is indispensable to be acquainted with the history of the meanings of Abbildung. This word was used in 1845 by Gauss for what is called in English a map-projection, which is an incorrect term, since many such modes of representation are not geometrical rectilinear projections at all; and of those which Gauss had in view, but a single one is so. In mathematics Abbildung is translated representation; but this word is preempted in logic. Since Bild is always translated image, imaging will answer very well for Abbildung. If a map of the entire globe were made on a sufficiently large scale, and out of doors, the map itself would be shown upon the map; and upon that image would be seen the map of the map; and so on, indefinitely. If the map were to cover the entire globe, it would be an image of nothing but itself, where each point would be imaged by some other point, itself imaged by a third, &c. But a map of the heavens does not show the map itself at all. A Mercator's projection shows the entire globe (except the poles) over and over again in endlessly recurring strips. Many maps, if they were completed, would show two or more different places on the earth at each point of the map (or at any rate on a part of it), like one map drawn upon another. Such is obviously the case with any rectilinear projection of the entire sphere, excepting only the stereographic. These two peculiarities may coexist in the same map.
Any mathematical function of one variable may be regarded as an image of its variable according to some mode of imaging. For the real and imaginary quantities correspond, one to one and continuously, to the assignable points on a sphere. Although mathematics is by far the swiftest of the sciences in its generalizations, it was not until 1879 that Dedekind (in the 3rd edition of his recension of Lejeune-Dirichlet's Zahlentheorie, § 163, p. 470; but the writer has not examined the second edition) extended the conception to discrete systems in these words: ‘It very often happens in other sciences, as well as in mathematics, that there is a replacement of every element ω of a system of elements or things by a corresponding element ω' [of a system Ω']. Such an act should be called a substitution. . . . But a still more convenient expression is found by regarding Ω' as the image of Ω, and ω' of ω, according to a certain mode of imaging.’ And he adds, in a footnote: ‘This power of the mind of comparing a thing ω with a thing ω', or of relating ω to ω', or of considering ω' to correspond to ω, is one without which no thought would be possible.’ [We do not translate the main clause.] This is an early and significant acknowledgment that the so-called ‘logic of relatives’—then deemed beneath the notice of logicians—is an integral part of logic. This remark remained unnoticed until, in 1895, Schröder devoted the crowning chapter of his great work (Exakte Logik, iii. 553-649) to its development. Schröder says that, in the broadest sense, any relative whatever may be considered as an imaging—‘nämlich als eine eventuell bald “undeutige,” bald “eindeutige,” bald “mehrdeutige” Zuordnung.’ He presumably means that the logical universe is thus imaged in itself. However, in a narrower sense, he says, a mode of imaging is restricted to a relative which fulfils one or other of the two conditions of being never undeutig, or being never mehrdeutig. That is, the relation must belong to one or other of the two classes, the one embracing such that every object has an image, and the other such that no object has more than one image. Schröder's definitions (however interesting his developments) break all analogy with the important property of the imaging of continua noticed above. If this is to be regarded as essential, an imaging must be defined as a generic relation between an object-class and an image-class, which generic relation consists of specific relations, in each of which one individual, and no more, of the image-class stands to each individual of the object-class, and in each of which every individual of the image-class stands to one individual, and to no more, of the object-class. This is substantially a return to Dedekind's definition, which makes an imaging a synonym for a substitution. (C.S.P., H.B.F.)
Implicit (in logic). Said of an element or character of a representation, whether verbal or mental, which is not contained in the representation itself, but which appears in the strictly logical (not merely in the psychological) analysis of that representation.
Thus, when we ordinarily think of something, say the Antarctic continent, as real, we do not stop to reflect that every intelligible question about it admits of a true answer; but when we logically analyse the meaning of reality, this result appears in the analysis. Consequently, only concepts, not percepts, can contain any implicit elements, since they alone are capable of logical analysis. An implicit contradiction, or contradiction in adjecto, is one which appears as soon as the terms are defined, irrespective of the properties of their objects. Thus there is, strictly speaking, no implicit contradiction in the notion of a quadrilateral triangle, although it is impossible. But, owing to exaggeration, this would currently be said to involve not merely an implicit, but an explicit contradiction, or contradiction in terms.
Any proposition which neither requires the exclusion from nor the inclusion in the universe of any state of facts or kind of object except such as a given second proposition so excludes or requires to be included, is implied in that second proposition in the logical sense of implication, no matter how different it may be in its point of view, or otherwise. It is a part of the meaning of the copula ‘is’ employed in logical forms of proposition, that it expresses a transitive relation, so that whatever inference from the proposition would be justified by the dictum de omni is implied in the meaning of the proposition. Nor could any rule be admitted as universally valid in formal logic, unless it were a part of the definition of one of the symbols used in formal logic. Accordingly, whatever can be logically deduced from any proposition is implied in it; and conversely. Whether what is implied will, or will not, be suggested by the contemplation of the proposition is a question of psychology. All that concerns logic is, whether all the facts excluded and required by the one proposition are among those so excluded or required by the other. (C.S.P.)
Inconsistency [Lat. in + con + sistere, to stand]: Ger. Unvereinbarkeit; Fr. inconsistance; Ital. incompatibilità. The relation between two assertions which cannot be true at once, though it may not be a direct contradiction; as between a statement of items and a statement of their total. Cf. CONSISTENCY.
A logical discrepancy, on the other hand, is a difference between two statements either difficult or impossible to reconcile with the credibility of both. It is said to be negative if one assertion omits an inseparable part of the fact stated in another; as when one witness testifies that A pointed a pistol at B, and another that A shot at B. It is positive if one asserts what the other denies. But even then it may often be conciliable (verträglich); that is, may not prove that either statement is in other respects untrustworthy. See Bachmann, Logik, §§ 214 ff.
‘Inconsistent’ is applied to an assertion, or hypothesis, which either in itself, or in copulation with another proposition with which it is said to be inconsistent, might be known to be false by a man devoid of all information except the meanings of the words used and their syntax.
Inconsistent differs from contradictory (see CONTRADICTION) in being restricted usually to propositions, expressed or implied, and also in not implying that the falsity arises from a relation of negation. ‘That is John’ and ‘It is Paul’ are inconsistent, but hardly contradictory. Moreover, contradictory is also used in a peculiar sense in formal logic. Cf. OPPOSITION. (C.S.P.)
Independence [Lat. in + de + pendere, to hang]: Ger. Unabhängigkeit; Fr. indépendance; Ital. indipendenza. (1) Two subjects are independent in so far as the possession of any character by the one does not require nor prevent the possession of any character by the other, unless these characters are directly or indirectly relative to the other individual.
(2) Two events are independent if either is equally probable whether the other takes place or not. (C.S.P.)
Index (in exact logic). A sign, or representation, which refers to its object not so much because of any similarity or analogy with it, nor because it is associated with general characters which that object happens to possess, as because it is in dynamical (including spatial) connection both with the individual object, on the one hand, and with the senses or memory of the person for whom it serves as a sign, on the other hand.
No matter of fact can be stated without the use of some sign serving as an index. If A says to B, ‘There is a fire,’ B will ask, ‘Where?’ Thereupon A is forced to resort to an index, even if he only means somewhere in the real universe, past and future. Otherwise, he has only said that there is such an idea as fire, which would give no information, since unless it were known already, the word ‘fire’ would be unintelligible. If A points his finger to the fire, his finger is dynamically connected with the fire, as much as if a self-acting fire-alarm had directly turned it in that direction; while it also forces the eyes of B to turn that way, his attention to be riveted upon it, and his understanding to recognize that his question is answered. If A's reply is, ‘Within a thousand yards of here,’ the word ‘here’ is an index; for it has precisely the same force as if he had pointed energetically to the ground between him and B. Moreover, the word ‘yard,’ though it stands for an object of a general class, is indirectly indexical, since the yard-sticks themselves are signs of the Parliamentary Standard, and that, not because they have similar qualities, for all the pertinent properties of a small bar are, as far as we can perceive, the same as those of a large one, but because each of them has been, actually or virtually, carried to the prototype and subjected to certain dynamical operations, while the associational compulsion calls up in our minds, when we see one of them, various experiences, and brings us to regard them as related to something fixed in length, though we may not have reflected that that standard is a material bar. The above considerations might lead the reader to suppose that indices have exclusive reference to objects of experience, and that there would be no use for them in pure mathematics, dealing, as it does, with ideal creations, without regard to whether they are anywhere realized or not. But the imaginary constructions of the mathematician, and even dreams, so far approximate to reality as to have a certain degree of fixity, in consequence of which they can be recognized and identified as individuals. In short, there is a degenerate form of observation which is directed to the creations of our own minds—using the word observation in its full sense as implying some degree of fixity and quasi-reality in the object to which it endeavours to conform. Accordingly, we find that indices are absolutely indispensable in mathematics; and until this truth was comprehended, all efforts to reduce to rule the logic of triadic and higher relations failed; while as soon as it was once grasped the problem was solved. The ordinary letters of algebra that present no peculiarities are indices. So also are the letters A, B, C, &c., attached to a geometrical figure. Lawyers and others who have to state a complicated affair with precision have recourse to letters to distinguish individuals. Letters so used are merely improved relative pronouns. Thus, while demonstrative and personal pronouns are, as ordinarily used, ‘genuine indices,’ relative pronouns are ‘degenerate indices’; for though they may, accidentally and indirectly, refer to existing things, they directly refer, and need only refer, to the images in the mind which previous words have created.
Indices may be distinguished from other signs, or representations, by three characteristic marks: first, that they have no significant resemblance to their objects; second, that they refer to individuals, single units, single collections of units, or single continua; third, that they direct the attention to their objects by blind compulsion. But it would be difficult, if not impossible, to instance an absolutely pure index, or to find any sign absolutely devoid of the indexical quality. Psychologically, the action of indices depends upon association by contiguity, and not upon association by resemblance or upon intellectual operations. See Peirce, in Proc. Amer. Acad. Arts and Sci., vii. 294 (May 14, 1867). (C.S.P.)
Individual (in logic) [as a technical term of logic, individuum first appears in Boethius, in a translation from Victorinus, no doubt of ἀτομον, a word used by Plato (Sophistes, 229 D) for an indivisible species, and by Aristotle, often in the same sense, but occasionally for an individual. Of course the physical and mathematical senses of the word were earlier. Aristotle's usual term for individuals is τα καθ’ ἑκαστα, Lat. singularia, Eng. singulars.] Used in logic in two closely connected senses. (1) According to the more formal of these an individual is an object (or term) not only actually determinate in respect to having or wanting each general character and not both having and wanting any, but is necessitated by its mode of being to be so determinate. See PARTICULAR (in logic).
This definition does not prevent two distinct individuals from being precisely similar, since they may be distinguished by their heceeities (or determinations not of a generalizable nature); so that Leibnitz' principle of indiscernibles is not involved in this definition. Although the principles of contradiction and excluded middle may be regarded as together constituting the definition of the relation expressed by ‘not,’ yet they also imply that whatever exists consists of individuals. This, however, does not seem to be an identical proposition or necessity of thought; for Kant's Law of Specification (Krit. d. reinen Vernunft, 1st ed., 656; 2nd ed., 684; but it is requisite to read the whole section to understand his meaning), which has been widely accepted, treats logical quantity as a continuum in Kant's sense, i.e. that every part of which is composed of parts. Though this law is only regulative, it is supposed to be demanded by reason, and its wide acceptance as so demanded is a strong argument in favour of the conceivability of a world without individuals in the sense of the definition now considered. Besides, since it is not in the nature of concepts adequately to define individuals, it would seem that a world from which they were eliminated would only be the more intelligible. A new discussion of the matter, on a level with modern mathematical thought and with exact logic, is a desideratum. A highly important contribution is contained in Schröder's Logik, iii, Vorles. 10. What Scotus says (Quaest. in Met., VII. 9, xiii and xv) is worth consideration.
(2) Another definition which avoids the above difficulties is that an individual is something which reacts. That is to say, it does react against some things, and is of such a nature that it might react, or have reacted, against my will.
This is the stoical definition of a reality; but since the Stoics were individualistic nominalists, this rather favours the satisfactoriness of the definition than otherwise. It may be objected that it is unintelligible; but in the sense in which this is true, it is a merit, since an individual is unintelligible in that sense. It is a brute fact that the moon exists, and all explanations suppose the existence of that same matter. That existence is unintelligible in the sense in which the definition is so. That is to say, a reaction may be experienced, but it cannot be conceived in its character of a reaction; for that element evaporates from every general idea. According to this definition, that which alone immediately presents itself as an individual is a reaction against the will. But everything whose identity consists in a continuity of reactions will be a single logical individual. Thus any portion of space, so far as it can be regarded as reacting, is for logic a single individual; its spatial extension is no objection. With this definition there is no difficulty about the truth that whatever exists is individual, since existence (not reality) and individuality are essentially the same thing; and whatever fulfils the present definition equally fulfils the former definition by virtue of the principles of contradiction and excluded middle, regarded as mere definitions of the relation expressed by ‘not.’ As for the principle of indiscernibles, if two individual things are exactly alike in all other respects, they must, according to this definition, differ in their spatial relations, since space is nothing but the intuitional presentation of the conditions of reaction, or of some of them. But there will be no logical hindrance to two things being exactly alike in all other respects; and if they are never so, that is a physical law, not a necessity of logic. This second definition, therefore, seems to be the preferable one. Cf. PARTICULAR (in logic). (C.S.P.)
Inference [Lat. in + ferre, to bear]: Ger. Schliessen, Schluss; Fr. inférence; Ital. illazione (conclusione). (1) In logic: (a) the act of consciously determining the content of a cognition by a previous cognition or cognitions, in a way which seems generally calculated to advance knowledge.
In this sense the word differs from REASONING (q.v.) only in referring strictly to a single step of the process, or to what seems a single step. Unless the act is consciously performed, no logical control can be exercised; and this is sufficient reason for separating such acts from any operations otherwise analogous which may take place in the formation of percepts. To be conscious of determining a cognition by another, and not merely of making the one follow after the other, involves some more or less obscure judgment that the pair of representations, the determining and determined, belong to a class of analogous pairs, so that a general maxim is virtually obeyed in the act. There is, besides, a purpose of learning more of the truth. The representations concerned in inference are, it appears, always judgments (or propositions). Probably, if a pair of percepts were, in the very act of determining the one to accord with the other, looked upon as special cases of a class of pairs of percepts so related to one another that if one were true the other ought to be accepted, they would, ipso facto, become judgments.
(b) A pair (or larger set) of judgments, of which one (or all of them together but one) determines the remaining one, as in (a) above, the whole set being regarded as constituting together a cognition more complete than a judgment.
In this sense, inference is synonymous with argument. The latter word, it is true, only implies that the set of propositions might be thought, being perhaps written down and no longer even accepted by the author, while the former word implies that the movement of thought takes place. Moreover, an inference creates belief in the mind that makes it, while an argument may be a system of propositions put together with a view of creating belief in another mind, or perhaps merely to exhibit the logical relation between different beliefs. But these distinctions often vanish or lose all importance. When the determining judgment is a copulative proposition, its members may either be called the premises, or their compound may be called the PREMISE (q.v.). But when different beliefs are brought together in thought for the first time to form a copulative judgment, the premises must be taken as plural.
Several other logical meanings are in general use as more or less permissible inaccuracies of language. Thus, the determined judgment, or conclusion, may sometimes be conveniently called an ‘inference.’ The popular use of the word for a dubious illation, as in such a sentence as ‘This is a proof positive, while that is only an inference,’ is quite inadmissible. (C.S.P.)
Insolubilia [Lat. in + solvere, to loose; trans. of Aristotle's ἀπορια; used mainly in plural]. A class of sophisms in which a question is put of such a nature that, whether it be answered affirmatively or negatively, an argument unimpeachable in form will prove the answer to be false.
The type is this: Given the following proposition:
Whatever is asserted in it is true,
But that it is not true is asserted in it;
\ By Barbara, That it is not true is true;
\ It is not true.
Besides, if it is true, that it is true is true. Hence,
That it is not true is not true,
But that it is not true is asserted in the proposition;
\ By Darapti, Something asserted in the proposition is not true;
\ The proposition is not true.
On the other hand, suppose it is not true. In that case,
That it is not true is true,
But all that the proposition asserts is that it is not true;
\ By Barbara, All that the proposition asserts is true;
\ The proposition is true.
Besides, in this case,
Something the proposition asserts is not true,
But all that the proposition asserts is that it is not true;
\ By Bokardo, That it is not true is not altogether true;
\ That it is true is true;
\ it is true.
Thus, whether it be true or not, it is both true and not. Now, it must be either true or not, hence it is both true and not, which is absurd.
Only two essentially distinct methods of solution have been proposed. One, which is supported by Ockham (Summa totius logices, 3rd div. of 3rd part, cap. 38 and 45), admits the validity of the argumentation and its consequence, which is that there can be no such proposition, and attempts to show by other arguments that no proposition can assert anything of itself. Many logical writers follow Ockham in the first part of his solution, but fail to see the need of the second part. The other method of solution, supported by Paulus Venetus (Sophismata Aurea, sophisma 50), diametrically denies the principle of the former solution, and undertakes to show that every proposition virtually asserts its own truth. This method, therefore, denies the premise of the antithesis that ‘all that the proposition asserts is that it is not true,’ since, like every other proposition, it also asserts its own truth, and is therefore contradictory and false, not in what it expressly asserts, but in what it implicitly asserts. Some writers (as Fries) hold that because every proposition asserts its own truth, therefore nothing is a proposition which asserts its own falsity. See Aristotle, Sophisticae Elenchi, cap. 25. Other proposed solutions of little importance are given by Paulus Venetus, loc. cit. (C.S.P.)
Intention (in logic) [Lat. intentio, with the same meaning in Aquinas (Summa Theol., I. 9. 53, is the principal passage); in classical writers an act of attention (and so Aquinas, ibid., I. ii. 9. 38, art. 2, and elsewhere); from in + tendere, to stretch. Aquinas seems sometimes to use the term for a mode of being (ibid., I. ii. 9. 22) and sometimes for a relation (ibid., I. 9. 29 art. 1; 9. 76, art. 3, and esp art. 4)]. A concept, as the result of attention.
First intentions are those concepts which are derived by comparing percepts, such as ordinary concepts of classes, relations, &c. Second intentions are those which are formed by observing and comparing first intentions. Thus the concept ‘class’ is formed by observing and comparing class-concepts and other objects. The special class-concept, ens, or what is, in the sense of including figments as well as realities, can only have originated in that way. Of relative second intentions, four are prominent—identity, otherness, co-existence, and incompossibility. Aquinas defined logic as the science of second intentions applied to first. (C.S.P.)
Involution [Lat. in + volvere, to roll]: Ger. Involution; Fr. involution; Ital. involuzione. A term of SYMBOLIC LOGIC (q.v. borrowed from algebra, where it means the raising of a base to a power. In logic it has two different senses. (1) Relative involution: let lwm denote any lover of a well-wisher of a man. That is, any individual A is denoted by lwm, provided there are in existence individuals B and C (who may be identical with each other or with A), such that A loves B, while B wishes well to C, and C is a man. Further, let lwm denote any individual A, if, and only if, there is in existence an individual C, who is a man, and who is such that taking any individual B whatever, if B is a well-wisher of C, then A is a lover B. The operation of combining l and w in this statement is termed ‘progressive involution.’ Again, let lwm denote any individual A, if, and only if, there is in existence an individual B, who is loved by A, and who is such that taking any individual C whatever, if C is wished well by B, then C is a man. The operation of combining w and m in this statement is termed ‘regressive involution.’ These designations were adopted because of the analogy of the general formulae to those of involution in the algebra of quantity.
These kinds of involution are not, at present, in use in symbolical logic; but they are, nevertheless, useful, especially in developing the conception of continuity. These two kinds of involution together constitute relative involution.
(2) Non-relative involution: consisting in the repeated introduction of the same premise into a reasoning; as, for example, the half-dozen simple premises upon which the Theory of Numbers is based are introduced over and over again in the reasoning by which its myriad theorems are deduced. In exact logic the regular process of deduction begins by non-relatively multiplying together all the premises to make one conjunctive premise, from which whatever can be deduced by using those premises as often as they are introduced as factors, can be deduced by processes of ‘immediate inference’ from that single conjunctive premise. But the general character of the conclusion is found to depend greatly upon the number of times the same factor is multiplied in. From this circumstance the importance and the name of non-relative involution arise. (C.S.P.)
Kind [AS. cynd, nature, from cynde, natural; same root as Gr. γενος, Lat. genus]: Ger. Art (the word ‘kind’ is also used to translate Ger. Gattung, for which see HEGEL'S TERMINOLOGY); Fr. genre; Ital. genere, specie. Before ‘class’ acquired its logical signification in Queen Anne's reign, kind was sometimes used for any collection of objects having a common and peculiar general character, simple or complex.
Thus, in Blundevile's Arte of Logicke, we read: ‘Genus is a general kind which may be spoken of many things differing in special kind.’ At other times, and more accurately, it was restricted to the species, or narrowest recognized class, or that which was supposed to be derived from one stock. Thus Wilson's Rule of Reason (1551) has: ‘Genus is a general woorde, vnder the whiche diuerse kindes or sortes of thinges are comprehended.’
But before persons who picked their words had become ready to use ‘class’ as a mere logical extension, they had begun to avoid ‘kind,’ except when the emphasis of attention was placed upon the logical depth rather than the breadth. Watts's Logick (1724) illustrates this. This last is the ordinary popular sense of the word to-day; so that ‘of this kind,’ ‘of this nature,’ ‘of this character’ are interchangeable phrases. J. S. Mill, however, in his System of Logic, Bk. I. chap. vii. § 4, erected the word into a technical term of logic, at the same time introducing the term ‘real kind.’ His meaning, so far as it was determinate, was that classes are of two orders, the first comprising those which, over and above the characters which are involved in their definitions and which serve to delimit their extension, have, at most, but a limited number of others, and those following as ‘consequences, under laws of nature,’ of the defining characters; and the second, the real kinds, comprising those each of which has innumerable common properties independent of one another. As instances of real kinds, he mentions the class of animals and the class of sulphur; as an instance of a kind not real, the class of white things. It is important for the understanding of Mill's thought here, as throughout his work, to note that when he talks of ‘properties,’ he has in mind, mainly, characters interesting to us. Otherwise, it would not be true that all white things have few properties in common. By a ‘law of nature’ he means any absolute uniformity; so that it is hardly enough to assert that if all white things had any property P, this would be a ‘consequence, under a law of nature,’ of their whiteness; for it would be itself an absolute and ultimate uniformity. Mill says that if the common properties of a class thus follow from a small number of primary characters ‘which, as the phrase is, account for all the rest,’ it is not a real kind. He does not remark that the man of science is bent upon ultimately thus accounting for each and every property that he studies. The following definition might be proposed: Any class which, in addition to its defining character, has another that is of permanent interest and is common and peculiar to its members, is destined to be conserved in that ultimate conception of the universe at which we aim, and is accordingly to be called ‘real.’ (C.S.P.)
Knowledge (in logic). This word is used in logic in two senses: (1) as a synonym for COGNITION (q.v.), and (2), and more usefully, to signify a perfect cognition, that is, a cognition fulfilling three conditions: first, that it holds for true a proposition that really is true; second, that it is perfectly self-satisfied and free from the uneasiness of doubt; third, that some character of this satisfaction is such that it would be logically impossible that this character should ever belong to satisfaction in a proposition not true.
Knowledge is divided, firstly, according to whatever classification of the sciences is adopted. Thus, Kantians distinguish formal and material knowledge. See SCIENCE. Secondly, knowledge is divided according to the different ways in which it is attained, as into immediate and mediate knowledge. See IMMEDIACY AND MEDIACY (logical). Immediate knowledge is a cognition, or objective modification of consciousness, which is borne in upon a man with such resistless force as to constitute a guarantee that it (or a representation of it) will remain permanent in the development of human cognition. Such knowledge is, if its existence be granted, either borne in through an avenue of sense, external or internal, as a percept of an individual, or springs up within the mind as a first principle of reason or as a mystical revelation. Mediate knowledge is that for which there is some guarantee behind itself, although, no matter how far criticism be carried, simple evidency, or direct insistency, of something has to be relied upon. The external guarantee rests ultimately either upon authority, i.e. testimony, or upon observation. In either case mediate knowledge is attained by REASONING, which see for further divisions. It is only necessary to mention here that the Aristotelians distinguished knowledge ὁτι, or of the facts themselves, and knowledge διοτι, or of the rational connection of facts, the knowledge of the how and why (cf. the preceding topic). They did not distinguish between the how and the why, because they held that knowledge διοτι is solely produced by SYLLOGISM (q.v.) in its greatest perfection, as demonstration. The term empirical knowledge is applied to knowledge, mediate or immediate, which rests upon percepts; while the terms philosophical and rational knowledge are applied to knowledge, mediate or immediate, which rests chiefly or wholly upon conclusions or revelations of reason. Thirdly, knowledge is divided, according to the character of the immediate object, into apprehensive and judicative knowledge, the former being of a percept, image, or Vorstellung, the latter of the existence or non-existence of a fact. Fourthly, knowledge is divided, according to the manner in which it is in the mind, into actual, virtual, and habitual knowledge. See Scotus, Opus Oxoniense, lib. I. dist. iii. quest. 2, paragraph beginning ‘Loquendo igitur.’ Fifthly, knowledge is divided, according to its end, into speculative and practical. (C.S.P., C.L.F.)
Laws of Thought: Ger. Denkgesetze; Fr. lois de la pensée; Ital. leggi del pensiero. The three formulas of identity, contradiction, and excluded middle have been widely so known, though the doctrine that they are three co-ordinate and sufficient laws of all thought or of all reasoning has been held by a comparatively small party which hardly survives; and it is not too much to say that the doctrine is untenable. But the designation is so familiar and convenient that those formulas may very well be referred to as ‘the so-called three laws of thought.’ The formulas have usually been stated by those who upheld the doctrine as follows:—
I. The Principle of Identity: A is A.
II. The Principle of Contradiction: A is not not-A.
III. The Principle of Excluded Middle or Excluded Third:
everything is either A or not-A.
It is noticeable that two of these propositions are categorical and the third disjunctive, a circumstance demanding explanation for those who hold the distinction of categorical, conditional, and disjunctive propositions to be fundamental.
The meaning of the formula of identity presents only one small difficulty. If the copula ‘is’ be taken in the sense of ‘is, if it exists,’ then the meaning of the formula is that no universal affirmative proposition having the same term as subject and predicate is false. If, however, the copula be understood to imply existence, the meaning is that no universal affirmative proposition is false in which the same term is subject and predicate, provided that term denotes any existing object. Or, the meaning may be that the same thing is true when the subject and predicate are the same proper name of an individual. In any case, it may properly be required that the precise meaning attached to the copula should be explained; and this explanation must in substance involve one or other of the above three statements; so that in any case the principle of identity is merely a part of the definition of the copula.
In like manner, if the word ‘not’ is to be used in logical forms, its force should be explained with the utmost precision. Such an explanation will consist in showing that the relation it expresses belongs at once to certain classes of relations, probably not more than two, in view of the simplicity of the idea. Each of these two statements may be embodied in a formula similar, in a general way, to the formulas of contradiction and excluded middle. It has, therefore, seemed to Mill and to the ‘exact’ logicians that these two formulas ought together to constitute a definition of the force of ‘not.’
Other writers have regarded all three laws as ‘practical maxims.’ But practically nobody needs a maxim to remind him that a contradiction, for example, is an absurdity. It might be a useful injunction to tell him to beware of latent contradictions; but as soon as he clearly sees that a proposition is self-contradictory, he will have abandoned it before any maxim can be adduced. Seeing, then, that such formulas are required to define the relation expressed by not, but are not required as maxims, it is in the former aspect that their true meanings are to be sought.
If it is admitted that they constitute a definition, they must conform to the rules of definition. Considered as part of a definition, one of the commonest statements of the principle of contradiction, ‘A non est non-A,’ offends against the rule that the definitum must not be introduced into the definition. This is easily avoided by using the form ‘A est non non-A,’ ‘A is not not-A,’ or every term may be subsumed under the double negation of itself. If this form is adopted for the principle of contradiction, the principle of excluded middle ought to be ‘What is not not-A is A.’ If, however, we prefer to state the principle of excluded middle as ‘Everything is either A or not-A,’ then we should state the principle of contradiction as ‘What is, at once, A and not-A is nothing.’ There is no vicious circle here, since the term ‘nothing,’ or ‘non ens,’ may be formally defined without employing the particle ‘not’ or any equivalent. Thus, we may express the principle of contradictions as follows:
Whatever there may be which is both A and not-A is X, no matter what term X may be.In either formula, A may be understood to be restricted to being an individual, or it may be allowed to be any term, individual or general. In the former case, in order to avoid conflict with the fundamental law that no true definition asserts existence, a special clause should be added, such as ‘if not-A there be.’ In the latter case, it should be stated that by ‘not-A’ is not meant ‘not some A,’ but ‘not any A,’ or ‘other than whatever A there may be.’
Bearing these points in mind, the formula ‘A is not-not-A,’ or ‘A is other than whatever is other than whatever is A,’ is seen to be a way of saying that the relation expressed by ‘not’ is one of those which is its own converse, and is analogous to the following:
Every rose is similar to whatever is similar to whatever is a rose;which again is similar to the following:
Every man is loved by whatever loves whatever is a man.But if we turn to the corresponding formula of excluded middle, ‘Not-not-A is A,’ or ‘Whatever is not anything that is not any A is A,’ we find that its meaning cannot be so simply expressed. Supposing that the relation r is such that it is true that
Whatever is r to whatever is r to whatever is A is A,it can readily be proved that, whether the multitude of individuals in the universe be finite or infinite, each individual is either non-r to itself and to nothing else, or is one of a pair of individuals that are non-r to each other and to nothing else; and conversely, if the universe is so constituted, the above formula necessarily holds. But it is evident that if the universe is so constituted, the relation r is converse to itself; so that the formula corresponding to that of contradiction also holds. But this constitution of the universe does not determine r to be the relation expressed by ‘not.’ Hence, the pair of formulas,
A is not not-A,are inadequate to defining ‘not,’ and the former of them is mere surplusage. In fact, in a universe of monogamously married people taking any class, the A's,
Not not-A is A,
Every A is a non-spouse to whatever is non-spouse to every A,and
Whatever is non-spouse to whatever is a non-spouse to every A is an A.No such objection exists to the other pair of formulas:
Whatever is both A and not-A is nothing,Their meaning is perfectly clear. Dividing all ordered pairs of individuals into those of the form A : B and those of the form A : A,
Everything is either A or not-A.
The principle of contradiction excludes from the relation ‘not’ all of the form A : A,
The principle of excluded middle makes the relation of ‘not’ to include all pairs of the form A:B.
From this point of view, we see at once that there are three other similar pairs of formulas defining the relations of identity, coexistence, and incompossibility, as follows:
Whatever is A is identical with A; i.e. Identity includes all pairs A : A.
Whatever is identical with A is A; i.e. Identity excludes all pairs A : B.
Whatever is A is coexistent with A; i.e. Coexistence includes all pairs A : A.
Everything is either A or coexistent with A; i.e. Coexistence includes all pairs A : B.
Whatever is both A and incompossible with A is nothing; i.e. Incompossibility excludes all pairs A : A.
Whatever there may be incompossible with A is A; i.e. Incompossibility excludes all pairs A : B.
Much has been written concerning the relations of the three principles to forms of syllogism. They have even been called Die Principien des Schliessens, and have often been so regarded. Some points in reference to the meanings they have borne in such discussions require mention. Many writers have failed to distinguish sufficiently between reasoning and the logical forms of inference. The distinction may be brought out by comparing the moods Camestres and Cesare (see MOOD, in logic). Formally, these are essentially different. The form of Camestres is as follows:
Every P is an M,This form does not depend upon either clause of the definition of ‘not’ or ‘other than.’ For if any other relative term, such as ‘lover of,’ be substituted for ‘other than,’ the inference will be equally valid. The form of Cesare is as follows:
Every S is other than every M;
\ Every S is other than every P.
Every P is other than every M,This depends upon the equiparance of ‘other than.’ For if we substitute an ordinary relative, such as loves, for ‘other than’ in the premise, the conclusion will be
Every S is an M;
\ Every S is other than every P.
Every S is loved by every P.(See De Morgan's fourth memoir on the syllogism, Cambridge Philos. Trans., x. (1860) 354.) The two forms are thus widely distinct in logic; and yet when a man actually performs an inference, it would be impossible to determine that he ‘reasons in’ one of these moods rather than in the other. Either statement is incorrect. He does not, in strict accuracy, reason in any form of syllogism. For his reasoning moves in first intentions, while the forms of logic are constructions of second intentions. They are diagrammatic representations of the intellectual relation between the facts from which he reasons and the fact which he infers, this diagram necessarily making use of a particular system of symbols—a perfectly regular and very limited kind of language. It may be a part of a logician's duty to show how ordinary ways of speaking and of thinking are to be translated into that symbolism of formal logic; but it is no part of syllogistic itself. Logical principles of inference are merely rules for the illative transformation of the symbols of the particular system employed. If the system is essentially changed, they will be quite different. As the Boolians represent Cesare and Camestres, they appear, after literally translating the algebraic signs of those logicians into words, as follows:
A that is B is nothing,The two moods are here absolutely indistinguishable.
C that is not B is nothing,
\ A that is Cis nothing.
From the time of Scotus down to Kant more and more was made of a principle agreeing in enunciation, often exactly, in other places approximately, with our principle of contradiction, and in the later of those ages usually called by that name, although earlier more often principium primum, primum cognitum, principium identitatis, dignitas dignitatum, &c. It would best be called the Principle of Consistency. Attention was called to it in the fourth book of Aristotle's Metaphysics. The meaning of this, which was altogether different, at least in post-scholastic times, from our principle of contradiction, is stated in the so-called Monadologie of Leibnitz (§ 31) to be that principle by virtue of which we judge that to be false which involves a contradiction, and the denial of the contradiction to be true. The latter clause involves an appeal to the principle of excluded middle as much as the former clause does to the formal principle of contradiction. And so the ‘principle of contradiction’ was formerly frequently stated. But, in fact, neither is appealed to; for Leibnitz does not say that the contradiction is to be made explicit, but only that it is to be recognized as an inconsistency. Interpreted too strictly, the passage would seem to mean that all demonstrative reasoning is by the reductio ad absurdum; but this cannot be intended. All that is meant is that we draw that conclusion the denial of which would involve an absurdity—in short, that which consistency requires. This is a description, however imperfect, of the procedure of demonstrative REASONING (q.v.), and does not relate to logical forms. It deals with first, not second, intentions. (C.S.P.)
It is unfortunate that ‘contradictory’ and ‘principle of contradiction’ are terms used with incongruent significations. If α and β are statements, they are mutually contradictory, provided that one or the other of them must be true and that both cannot be true; these are the two marks (essential and sufficient) of contradiction, or precise denial, as it might better be called. If a and b are terms, b is the precise negative of a (or the contradictory term to a), provided it takes in all of that which is other than a—that is, if everything must be one or the other (a or b) and if nothing can be both. These two properties constitute the definition of a pair of contradictories (whether terms or propositions), namely, they are mutually exclusive, and they are together exhaustive; expressed in the language of ‘exact logic,’ these properties are (writing  for the negative of x and + for or):
for the negative of x and + for or):

Together these properties constitute the requirements of contradiction or of exact negation; it is a very inelegant piece of nomenclature (besides that it leads to actual confusion) to refer to (1) alone as the ‘principle of contradiction.’ Better names for them are (1) exclusion and (2) exhaustion (in place of excluded middle). In the common phraseology we are obliged to commit the absurdity of saying that two terms or propositions may satisfy the ‘principle of contradiction’ and still not be contradictory (since they may lack the quality of being exhaustive). The mere fact that (1) has been called the principle of contradiction has given it a pretended superiority over the other which it by no means deserves; they are of equal importance in the conducting of reasoning processes. In fact, for every formal argument which rests upon (1) there is a corresponding argument which rests upon (2): thus in the case of the fundamental law of TRANSPOSITION (q.v.), which affirms the identity of these two propositions, (m) the student who is not a citizen is not a voter; (n) every student is either a citizen or not a voter; that (m) follows from (n) depends upon one of these principles, and that (n) follows from (m) depends upon the other. These two names, exhaustion and exclusion, have the great advantage that they permit the formation of adjectives; thus we may say that the test for the contradictoriness of two terms or propositions which are not on their face the negatives one of another is that they should be (1) mutually exclusive and (2) together exhaustive.
It may be noticed that if two terms are exhaustive but not exclusive, their negatives are exclusive but not exhaustive. Thus within the field of number, ‘prime’ and ‘even’ are exclusive (no number can be both) but not exhaustive (except in the limiting case of two, some numbers can be neither), while ‘not even’ and ‘not prime’ are exhaustive and not exclusive.
In the case of propositions, ‘contrary’ and ‘subcontrary’ are badly chosen names for the OPPOSITION (q.v.) of A and E, O and I, respectively, of the traditional logical scheme; they do not carry their meaning on their face, and hence are unnecessarily difficult for the learner to bear in mind. A and E should be said to be mutually exclusive (but not exhaustive), O and I to be conjointly exhaustive (but not exclusive). This relation of qualities is then seen to be a particular case merely of the above-stated general rule.
Again, ‘no a is b’ and ‘all a is b’ are exclusive but not exhaustive, while ‘some a is b’ and ‘some a is not b’ are exhaustive but not exclusive (provided in both cases that a exists).
Laws of thought is not a good name for these two characteristics; they should rather be called the laws (if laws at all) of negation. Properly speaking, the laws of thought are all the rules of logic; of these laws there is one which is of far more fundamental importance than those usually referred to under the name, namely, the law that if a is b and b is c, it can be concluded that a is c. This is the great law of thought, and everything else is of minor importance in comparison with it. It is singular that it is not usually enumerated under the name. Another law of thought of equal consequence with those usually so called is, according to Sigwart, the law that the double negative is equivalent to an affirmative,

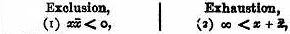
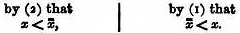 (C.L.F.)
(C.L.F.) Literature: for the history of these principles see UEBERWEG, Syst. d. Logik, §§ 75-80; PRANTL, Gesch. d. Logik (see ‘principium’ in the indices to the four volumes). There are additional notes in an appendix to HAMILTON, Lects. on Logic. (C.S.P.)
Leading of Proof: no concise foreign equivalents. The operation bringing up to attention, among propositions admitted to be true, certain relations between them which logically compel the acceptance of a conclusion. (C.S.P.)
Leading Principle: Ger. leitendes Prinzip; Fr. principe directeur; Ital. principio fondamentale. It is of the essence of reasoning that the reasoner should proceed, and should be conscious of proceeding, according to a general habit, or method, which he holds would either (according to the kind of reasoning) always lead to the truth, provided the premises were true; or, consistently adhered to, would eventually approximate indefinitely to the truth; or would be generally conducive to the ascertainment of truth, supposing there be any ascertainable truth. The effect of this habit or method could be stated in a proposition of which the antecedent should describe all possible premises upon which it could operate, while the consequent should describe how the conclusion to which it would lead would be determinately related to those premises. Such a proposition is called the ‘leading principle’ of the reasoning.
Two different reasoners might infer the same conclusion from the same premises; and yet their proceeding might be governed by habits which would be formulated in different, or even conflicting, leading principles. Only that man's reasoning would be good whose leading principle was true for all possible cases. It is not essential that the reasoner should have a distinct apprehension of the leading principle of the habit which governs his reasoning; it is sufficient that he should be conscious of proceeding according to a general method, and that he should hold that that method is generally apt to lead to the truth. He may even conceive himself to be following one leading principle when, in reality, he is following another, and may consequently blunder in his conclusion. From the effective leading principle, together with the premises, the propriety of accepting the conclusion in such sense as it is accepted follows necessarily in every case. Suppose that the leading principle involves two propositions, L and L', and suppose that there are three premises, P, P', P''; and let C signify the acceptance of the conclusion, as it is accepted, either as true, or as a legitimate approximation to the truth, or as an assumption conducive to the ascertainment of the truth. Then, from the five premises L, L', P, P', P'', the inference to C would be necessary; but it would not be so from L, L', P', P'' alone, for, if it were, P would not really act as a premise at all. From P' and P'' as the sole premises, C would follow, if the leading principle consisted of L, L', and P. Or from the four premises L', P, P', P'', the same conclusion would follow if L alone were the leading principle. What, then, could be the leading principle of the inference of C from all five propositions L, L', P, P', P'', taken as premises? It would be something already implied in those premises; and it might be almost any general proposition so implied. Leading principles are, therefore, of two classes; and any leading principle whose truth is implied in the premises of every inference which it governs is called a ‘logical’ (or, less appropriately, a formal) leading principle; while a leading principle whose truth is not implied in the premises is called a ‘factual’ (or material) leading principle. (C.S.P.)
Lemma [Gr. λημμα, gain, an assumption, premise]: Ger. Hilfssatz, Lehnsatz; Fr. lemme; Ital. lemma. A theorem which interrupts the course of development of a mathematical theory, but which is inserted to supply a premise for one of the theorems.
This use of the word seems to go back to Euclid, at least; and even Aristotle uses the word—not a common one with him—in connection with geometry, in the first chapter of the Topics. With Aristotle, however, it means a premise; and with the Stoics, more particularly, the major premise of a syllogism. (C.S.P.)
Light of Nature [trans. of Lat. lumen naturae or naturale, a term used by Aquinas, Summa Theologiae, Pt. I, qu. 12, art. 13, and elsewhere. It is not necessary to suppose that he borrowed the term from the passage of Aristotle's De Anima, 430 a, 14, where the creative intellect is compared with light]: Ger. natürliches Licht; Fr. lumière naturelle (Pascal); Ital. lume naturale (Galileo). A natural power, or instinct, by which men are led to the truth about matters which concern them, in anticipation of experience or revelation. See LUMEN (also for literature).
The phrase is used in contradistinction to supernatural light. Tucker's Light of Nature pursued is a book written as a mild reaction against Locke and the Associationalists in the direction of the philosophy of common sense. (C.S.P.)
Limitative [Lat. limitare, to enclose]: Ger. limitativ (Urtheil); Fr. limitatif; Ital. limitativo. (1) Applied to a third quality of judgments, additional to affirmative and negative. The idea of such a third quality originated among the Romans from the difference between ‘homo non est bonus’ and ‘homo est non bonus,’ the latter being the limitative.
(2) Setting limits in the sense (2) given under LIMITING NOTION (q.v.).
It is one of the numerous cases in which accidents of language have affected accepted logical forms without any good reason. Boethius and others applied the infinitation to the subject also, which De Morgan has shown makes a valuable addition to logic. Wolff, however, limited the modification to the predicate, without showing any serious reason for such application. Kant adopted it because it rounded out his triad of categories of quality. His defence, as reported by Jäsche, is that the negative excludes the subject from the sphere of the predicate, while the unendliche, limitative, or infinite judgment puts it into the infinite sphere outside the predicate. It is to be remarked that Kant regards a positive mark as differing per se from a negative one, and, in particular, as having a far narrower extension. Like most of the old logicians, he virtually limited the universe of marks to such as arrest our attention. If that had been explicitly and consistently done, it would have constituted an interesting particular logic, in which there would be a material and not merely formal difference between affirmative and negative facts. It is probable that Kant also understood the affirmative proposition to assert the existence of its subject, while the negative did not do so; so that ‘Some phoenixes do not rise from their ashes’ would be true, and ‘All phoenixes do rise from their ashes’ would be false. The limitative judgment would agree with the affirmative in this respect. This was probably his meaning, and he did not observe that his limitative judgment, ‘The human soul is immortal (nichtsterblich),’ may be construed as equivalent to the conjunctive judgment, ‘The human soul is not mortal, and it is the human soul.’ No doubt Kant would have seen a world of difference between these two assertions. In that case he should have adopted a fourth quality, ‘The human soul is not immortal.’ (C.S.P.)
Limiting Notion: Ger. Grenzbegriff; Fr. notion-limite; Ital. concetto limite. (1) A term used by Kant in a single passage of the Krit. d. reinen Vernunft (1st ed., 255) to signify that a NOUMENON (q.v., ad fin.), which is a thing in itself regarded as an object of reason, is something to which experience cannot attain, but is the inconceivable something behind the phenomena. The passage reads: ‘Der Begriff eines Noumenon ist also bloss ein Grenzbegriff, um die Anmassung der Sinnlichkeit einzuschränken, und also nur von negativem Gebrauche.’ (J.M.B.- C.S.P.)
Logic [Gr. λογικη]: Ger. Logik; Fr. logique; Ital. logica. Logic is a science which has not yet completed the stage of disputes concerning its first principles, although it is probably about to do so. Nearly a hundred definitions of it have been given. It will, however, generally be conceded that its central problem is the classification of arguments, so that all those that are bad are thrown into one division, and those which are good into another, these divisions being defined by marks recognizable even if it be not known whether the arguments are good or bad. Furthermore, logic has to divide good arguments by recognizable marks into those which have different orders of validity, and has to afford means for measuring the strength of arguments.
An approach to such a classification is made by every man whenever he reasons, in the proper sense of that term. It is true that the contemplation of a state of things believed to be real may cause the contemplator to believe something additional, without making any classification of such sequences. But in that case he does not criticize the procedure, nor so much as distinctly reflect that it is just. He can, consequently, not exercise any control over it. Now, that which is uncontrollable is not subject to any normative laws at all; that is, it is neither good nor bad; it neither subserves an end nor fails to do so. But it is only the deliberate adoption of a belief in consequence of the admitted truth of some other proposition which is, properly speaking, reasoning. In that case the belief is adopted because the reasoner conceives that the method by which it has been determined would either in no analogous case lead to a false conclusion from true premises, or, if steadily adhered to, would at length lead to an indefinite approximation to the truth, or, at least, would assure the reasoner of ultimately attaining as close an approach to the truth as he can, in any way, be assured of attaining. In all reasoning, therefore, there is a more or less conscious reference to a general method, implying some commencement of such a classification of arguments as the logician attempts. Such a classification of arguments, antecedent to any systematic study of the subject, is called the reasoner's logica utens, in contradistinction to the result of the scientific study, which is called logica docens. See REASONING.
That part of logic, that is, of logica docens, which, setting out with such assumptions as that every assertion is either true or false, and not both, and that some propositions may be recognized to be true, studies the constituent parts of arguments and produces a classification of arguments such as is above described, is often considered to embrace the whole of logic; but a more correct designation is Critic (Gr. κριτικη. According to Diogenes Laertius, Aristotle divided logic into three parts, of which one was προς κρισιν). This word, used by Plato (who divides all knowledge into epitactic and critic), was adopted into Latin by the Ramists, and into English by Hobbes and Locke. From the last it was taken into German by Kant, who always writes it Critik, the initial c being possibly a reminiscence of its English origin. At present it is written Kritik in German. Kant is emphatic in the expression of the wish that the word may not be confounded with critique, a critical essay (Ger. Kritik). [The forms Critique and Critic are used interchangeably in this work. (Cf. CRITICISM.) (J.M.B.)]
It is generally admitted that there is a doctrine which properly antecedes what we have called critic. It considers, for example, in what sense and how there can be any true proposition and false proposition, and what are the general conditions to which thought or signs of any kind must conform in order to assert anything. Kant, who first raised these questions to prominence, called this doctrine transcendentale Elementarlehre, and made it a large part of his Critic of the Pure Reason. But the Grammatica Speculativa of Scotus is an earlier and interesting attempt. The common German word is Erkenntnisstheorie, sometimes translated EPISTEMOLOGY (q.v.).
It is further generally recognized that another doctrine follows after critic, and which belongs to, or is closely connected with, logic. Precisely what this should contain is not agreed; but it must contain the general conditions requisite for the attainment of truth. Since it may be held to contain more, one hesitates to call it heuristic. It is often called Method; but as this word is also used in the concrete, methodic or methodeutic would be better.
For deciding what is good logic and what is bad, appeal is made by different writers to one or more, generally several, of these eight sources: to direct dicta of consciousness, to psychology, to the usages of language, to metaphysical philosophy, to history, to everyday observation, to mathematics, and to some process of dialectic. In the middle ages appeal was frequently made to authority.
The appeal to direct consciousness consists in pronouncing certain reasoning to be good or bad because it is felt to be so. This is a very common method. Sigwart, for example, bases all logic upon our invincible mental repulsion against contradiction, or, as he calls it, ‘the immediate feeling of necessity’ (Logic § 3, 2). Those who think it worth while to make any defence at all of this proceeding urge, in effect, that, however far the logician may push his criticisms of reasoning, still in doing so, he must reason, and so must ultimately rely upon his instinctive recognition of good and bad reasoning. Whence it follows that, in Sigwart's words, ‘every system of logic must rest upon this principle.’ It is, however, to be noted that among the dicta of direct consciousness, many pronounce certain reasonings to be bad. If, therefore, such dicta are to be relied upon, man not only usually has a tendency to reason right, but also sometimes has a tendency to reason wrong; and if that be so, the validity of a reasoning cannot consist in a man's having a tendency to reason in that way. Some say that the validity of reasoning consists in the ‘definitive dictum’ of consciousness; but it has been replied that certain propositions in Euclid were studied for two thousand years by countless keen minds, all of whom had an immediate feeling of evidence concerning their proofs, until at last flaws were detected in those proofs, and are now admitted by all competent persons; and it is claimed that this illustrates how far from possible it is to make direct appeal to a definitive pronouncement. Besides, say those who object to this method, all reasoning and inquiry expects that there is such a thing as the truth concerning whatever question may be under examination. Now, it is of the very essence of this ‘truth,’ the meaning of the expectation, that the ‘truth’ in no wise depends upon what any man to whom direct appeal can be made may opine about that question. A fortiori it does not depend upon whether I am satisfied with it or not. It is further insisted that there can be no genuine criticism of a reasoning until that reasoning is actually doubted; and no sooner is it actually doubted than we find that consciousness has revoked her dictum in its favour, if she ever made any. It is, indeed, maintained that so far from true is it that every system of logic must be based upon any instinctive recognition of good and bad reasoning, that it is quite impossible for any reasoning to be based upon such recognition in respect to that same reasoning. In reasoning, a man may feel sure he is right; but to ‘rest’ that confidence on nothing but itself is to rest it on nothing at all. If the fact that we must use our reasoning instinct in criticizing reasoning proves that we must appeal to nothing else in such criticism, it equally proves that we ought to follow the lead of that instinct without any logical control at all, which would be as much as to say that we ought not to reason at all. A man cannot criticize every part of his reasoning, since he cannot criticize the act of reasoning he is performing in the criticism, it is true. But he can criticize steps whose validity he doubts; and in doing so, ought to consider in what characters the validity of reasoning consists, and whether the reasoning in question possesses those characters.
Under an appeal to psychology is not meant every appeal to any fact relating to the mind. For it is, for logical purposes, important to discriminate between facts of that description which are supposed to be ascertained by the systematic study of the mind, and facts the knowledge of which altogether antecedes such study, and is not in the least affected by it; such as the fact that there is such a state of mind as doubt, and the fact that the mind struggles to escape from doubt. Even facts like these require to be carefully examined by the logician before he uses them as the basis of his doctrine. But many logicians have gone much further, and have avowedly based their systems upon one or another theory of psychology. Another class of logicians have professed to base logic upon a psychological theory of cognition. Of course, if this is done, such psychological doctrine is placed above logical criticism, or, at any rate, above logical support. For if the truth of a conclusion is known only from certain premises, it cannot be used to support those premises. Now, it may be doubted whether psychology is not, of all the special sciences, the one which stands most in need of appeal to a scientific logic.
Appeals to the usages of language are extremely common. They are made even by those who use algebraical notation in logic ‘in order to free the mind from the trammels of speech’ (Schröder, Logik, i. p. iii). It is difficult to see what can be hoped for from such a proceeding, unless it be to establish a psychological proposition valid for all minds. But to do this, it would be necessary to look beyond the small and very peculiar class of Aryan languages, to which the linguistic knowledge of most of those writers is confined. The Semitic languages, with which some of them are acquainted, are too similar to the Aryan greatly to enlarge their horizon. Moreover, even if other languages are examined, the value of any logical inferences from them is much diminished by the custom of our grammarians of violently fitting them to the Procrustean bed of Aryan grammar.
The objection which has been suggested to appeals to psychological results applies with far greater force to appeals to metaphysical philosophy, which, it will generally be conceded, can hardly take a step with security unless it rests upon the science of logic. Nevertheless, a great many logical treatises of various colours make it their boast that they are built upon philosophical principles.
Logicians occasionally appeal to the history of science. Such and such a mode of reasoning, it is said, for example, was characteristic of mediaevalism or of ancient science; such another produced the successes of modern science. If logic is to be based upon probable reasonings, as some logicians maintain that it must be, such arguments, if critically examined, must be admitted to have great weight. They will naturally be out of place in a system of logic which professes to demonstrate from certain initial assumptions that the kinds of reasoning it recommends must be accepted.
There is probably room for dispute as to whether logic need assert anything at all as an absolute matter of fact. If it does not, any appeal to experience would seem to be irrelevant. If it does, still the opinion may be that such assertions of logic are of so exceedingly broad and slight a nature that the universal experience of every man's every day and hour puts them beyond all doubt—such experiences as that the world presents appearances of variety, of law, and of the real action of one thing upon another. As appearances, these things do not seem likely ever to be doubted. If logic has need of any facts, and if such facts will suffice, no objection can well be made to an appeal to them.
The boundary between some parts of logic and pure mathematics in its modern treatment is almost evanescent, as may be seen in Dedekind's Was sind und was sollen die Zahlen (1888, Eng. trans. 1901). There are, however, departments of logic, such as the logic of probable inference (if that be regarded a part of logic), in which appeal is sometimes made to mathematical results, such as Bernoulli's law of high numbers. It seems to be the general opinion that nothing so difficult as mathematics can be admitted into, or be appealed to by, the science of logic, which has the peculiarity of consisting chiefly of truisms.
In mathematical reasoning there is a sort of observation. For a geometrical diagram or array of algebraical symbols is constructed according to an abstractly stated precept, and between the parts of such diagram or array certain relations are observed to obtain, other than those which were expressed in the precept. These being abstractly stated, and being generalized, so as to apply to every diagram constructed according to the same precept, give the conclusion. Some logicians hold that an equally satisfactory method depends upon a kind of inward observation, which is not mathematical, since it is not diagrammatic, the development of a conception and its inevitable transformation being observed and generalized somewhat as in mathematics; and those logicians base their science upon such a method, which may conveniently be termed, and is sometimes termed, a Dialectic. Other logicians regard such a method as either extremely insecure or as altogether illusory.
The generally received opinion among professors of logic is that all the above methods may properly be used on occasion, the appeal to mathematics, however, being less generally recognized.
Literature: the history of logic in Western Europe, down to the revival of learning, is given by PRANTL, Gesch. d. Logik im Abendlande. Upon the points upon which this author touches, he always affords valuable information, though his judgments are peremptory and slashing. Unfortunately, he omits much which was regarded by the authors of whom he treats as most important, because he does not himself so regard it. He also omits much which would be interesting to a reader taking a broader conception of logic. It is hardly necessary to say that upon some large subjects his views are controverted. Of the modern development of logic there is no satisfactory history; but there are notices good as far as they go in UEBERWEG, Syst. d. Logik (Eng. trans.); in the much earlier work of BACHMANN, Syst. d. Logik (1828); in HAMILTON, Lects. on Logic; and for later work in B. ERDMANN, Logik. CH. SIGWART, Logic (Eng. trans.), and WUNDT, Logik, may also be profitably consulted. See under the logical topics generally (e.g. EMPIRICAL LOGIC, FORMAL LOGIC, JUDGMENT, and PROPOSITION); and also BIBLIOG. C. (C.S.P., C.L.F.)
Logic (exact): Ger. exakte Logik; Fr. logique exacte; Ital. logica esatta. The doctrine that the theory of validity and strength of reasoning ought to be made one of the ‘exact sciences,’ that is, that generalizations from ordinary experience ought, at an early point in its exposition, to be stated in a form from which by mathematical, or expository, REASONING (q.v.), the rest of the theory can be strictly deduced; together with the attempt to carry this doctrine into practice.
This method was pursued, in the past, by Pascal (1623-62), Nicolas Bernoulli (1687-1759), Euler (1708-83), Ploucquet (1716-90), Lambert (1728-77), La Place (1749-1827), De Morgan (1806-71), Boole (1815-64), and many others; and a few men in different countries continue the study of the problems opened by the last two named logicians, as well as those of the proper foundations of the doctrine and of its application to inductive reasoning. The results of this method, thus far, have comprised the development of the theory of probabilities, the logic of relatives, advances in the theory of inductive reasoning (as it is claimed), the syllogism of transposed quantity, the theory of the Fermatian inference, considerable steps towards an analysis of the logic of continuity and towards a method of reasoning in topical geometry, contributions towards several branches of mathematics by applications of ‘exact’ logic, the logical graphs called after Euler and other systems for representing in intuitional form the relations of premises to conclusions, and other things of the same general nature.
There are those, not merely outside the ranks of exact logic, but even within it, who seem to suppose that the aim is to produce a calculus, or semi-mechanical method, for performing all reasoning, or all deductive inquiry; but there is no reason to suppose that such a project, which is much more consonant with the ideas of the opponents of exact logic than with those of its serious students, can ever be realized. The real aim is to find an indisputable theory of reasoning by the aid of mathematics. The first step in the order of logic towards this end (though not necessarily the first in the order of inquiry) is to formulate with mathematical precision, definiteness, and simplicity, the general facts of experience which logic has to take into account.
The employment of algebra in the investigation of logic is open to the danger of degenerating into idle trifling of too rudimentary a character to be of mathematical interest, and too superficial to be of logical interest. It is further open to the danger that the rules of the symbols employed may be mistaken for first principles of logic. An algebra which brings along with it hundreds of purely formal theorems of no logical import whatever must be admitted, even by the inventor of it, to be extremely defective in that respect, however convenient it may be for certain purposes. On the other hand, it is indisputable that algebra has an advantage over speech in forcing us to reason explicitly and definitely, if at all. In that way it may afford very considerable aid to analysis. It has been employed with great advantage in the analysis of mathematical reasonings.
Algebraic reasoning involves intuition just as much as, though more insidiously than, does geometrical reasoning; and for the investigation of logic it is questionable whether the method of graphs is not superior. Graphs cannot, it is true, readily be applied to cases of great complexity; but for that very reason they are less liable to serve the purposes of the logical trifler. In the opinion of some exact logicians, they lead more directly to the ultimate analysis of logical problems than any algebra yet devised. See LOGICAL DIAGRAM (or GRAPH).
It is logical algebra, however, which has chiefly been pursued. De Morgan invented a system of symbols, which had the signal advantage of being entirely new and free from all associations, misleading or otherwise. Although he employed them for synthetical purposes almost exclusively, yet the great generality of some of the conceptions to which they led him is sufficient to show that they might have been applied with great advantage in analysis. Boole was led, no doubt from the consideration of the principles of the calculus of probabilities, to a wonderful application of ordinary algebra to the treatment of all deductive reasoning not turning upon any relations other than the logical relations between non-relative terms. By means of this simple calculus, he took some great steps towards the elucidation of probable reasoning; and had it not been that, in his pre-Darwinian day, the notion that certain subjects were profoundly mysterious, so that it was hopeless, if not impious, to seek to penetrate them, was still prevalent in Great Britain, his instrument and his intellectual force were adequate to carrying him further than he actually went. Most of the exact logicians of to-day are, from the nature of the case, followers of Boole. They have modified his algebra by disusing his addition, subtraction, and division, and by introducing a sign of logical aggregation. This was first done by Jevons; and he proposed .|. , a sign of division turned up, to signify this operation. Inasmuch as this might easily be read as three signs, it would, perhaps, be better to join the two dots by a light curve, thus Y. Some use the sign + for logical aggregation. The algebra of Boole has also been amplified so as to fit it for the logic of relatives. The system is, however, far from being perfect. See RELATIVES (logic of).
Certain terms of exact logic may be defined as follows:—
Aggregation. The operation of uniting two or more terms or propositions, called aggregants, to produce an aggregate term or proposition which is true of everything of which any aggregant is true, and false of everything of which all the aggregants are false. It is opposed to composition, which is the operation of producing from two or more terms or propositions, called the components, a new term or proposition, called their compound, which is true of all of which all the components are true, and false of all of which any are false.
Absorption, law of (Ger. Absorptionsgesetz). The proposition that if of two aggregants one contains the other as a component, the aggregate is identical with the latter.
Alternative proposition. A term preferred by some logicians to ‘disjunctive,’ because the latter term is often, as by Cicero and Aulus Gellius, understood to imply that one, and one only, of the alternatives is true. At the same time, the standard traditional example of a disjunctive was ‘Socrates currit vel Plato disputat,’ and the rule was ‘Ad veritatem disiunctivae sufficit alteram partem esse veram.’ Nevertheless, the narrower sense was also recognized, and the term alternative is perhaps preferable.
Associative. An operation combining two elements is associative if, and only if, in combining the result with a third element, it makes no difference whether the middle element be first combined with the last and the result with the first, or the other way, so long as the order of sequence is preserved. Addition and multiplication are associative, while involution is not so; for ten to the three-square power is a milliard, while ten cube squared is only a million. An associative algebra is an algebra in which multiplication is associative.
Commutative. An operation by which two elements are united is said to be commutative if, and only if, it makes no difference which is taken first. Thus, because twice three is thrice two, numerical multiplication is commutative.
Composition: see Aggregation, above.
Compound: see Aggregation, above.
Copula is often defined as that which expresses the relation between the subject-term and the predicate-term of a proposition. But this is not sufficiently accurate for the purposes of exact logic. Passing over the objection that it applies only to categorical propositions, as if conditional and copulative propositions had no copula, contrary to logical tradition, it may be admitted that a copula often does fulfil the function mentioned; but it is only an accidental one, and its essential function is quite different. Thus, the proposition ‘Some favoured patriarch is translated’ is essentially the same as ‘A translated favoured patriarch is’; and ‘Every mother is a lover of that of which she is a mother’ is the same as ‘A mother of something not loved by her is not.’ In the second and fourth forms, the copula connects no terms; but if it is dropped, we have a mere term instead of a proposition. Thus the essential office of the copula is to express a relation of a general term or terms to the universe. The universe must be well known and mutually known to be known and agreed to exist, in some sense, between speaker and hearer, between the mind as appealing to its own further consideration and the mind as so appealed to, or there can be no communication, or ‘common ground,’ at all. The universe is, thus, not a mere concept, but is the most real of experiences. Hence, to put a concept into relation to it, and into the relation of describing it, is to use a most peculiar sort of sign or thought; for such a relation must, if it subsist, exist quite otherwise than a relation between mere concepts. This, then, is what the copula essentially does. This it may do in three ways: first, by a vague reference to the universe collectively; second, by a reference to all the individuals existent in the universe distributively; third, by a vague reference to an individual of the universe selectively. ‘It is broad daylight,’ I exclaim, as I awake. My universe is the momentary experience as a whole. It is that which I connect as object of the composite photograph of daylight produced in my mind by all my similar experiences. Secondly, ‘Every woman loves something’ is a description of every existing individual in the universe. Every such individual is said to be coexistent only with what, so far as it is a woman at all, is sure to be a lover of some existing individual. Thirdly, ‘Some favoured patriarch is translated’ means that a certain description applies to a select individual. A hypothetical proposition, whether it be conditional (of which the alternative, or disjunctive, proposition is a mere species, or vice versa, as we choose to take it) or copulative, is either general or ut nunc. A general conditional is precisely equivalent to a universal categorical. ‘If you really want to be good, you can be,’ means ‘Whatever determinate state of things may be admissibly supposed in which you want to be good is a state of things in which you can be good.’ The universe is that of determinate states of things that are admissable hypothetically. It is true that some logicians appear to dispute this; but it is manifestly indisputable. Those logicians belong to two classes: those who think that logic ought to take account of the difference between one kind of universe and another (in which case, several other substantiae of propositions must be admitted); and those who hold that logic should distinguish between propositions which are necessarily true or false together, but which regard the fact from different aspects. The exact logician holds it to be, in itself, a defect in a logical system of expression, to afford different ways of expressing the same state of facts; although this defect may be less important than a definite advantage gained by it. The copulative proposition is in a similar way equivalent to a particular categorical. Thus, to say ‘The man might not be able voluntarily to act otherwise than physical causes make him act, whether he try or not,’ is the same as to say that there is a state of things hypothetically admissible in which a man tries to act one way and voluntarily acts another way in consequence of physical causes. As to hypotheticals ut nunc, they refer to no range of possibility, but simply to what is true, vaguely taken collectively.
Although it is thus plain that the action of the copula in relating the subject-term to the predicate-term is a secondary one, it is nevertheless necessary to distinguish between copulas which establish different relations between these terms. Whatever the relation is, it must remain the same in all propositional forms, because its nature is not expressed in the proposition, but is a matter of established convention. With that proviso, the copula may imply any relation whatsoever. So understood, it is the abstract copula of De Morgan (Camb. Philos. Trans., x. 339). A transitive copula is one for which the mood Barbara is valid. Schröder has demonstrated the remarkable theorem that if we use IS in small capitals to represent any one such copula, of which ‘greater than’ is an example, then there is some relative term r, such that the proposition ‘S IS P’ is precisely equivalent to ‘S is r to P and is r to whatever P is r to.’ A copula of correlative inclusion of one for which both Barbara and the formula of identity hold good. Representing any one such copula by is in italics, there is a relative term r, such that the proposition ‘S is P’ is precisely equivalent to ‘S is r to whatever P is r to.’ If the last proposition follows from the last but one, no matter what relative r may be, the copula is called the copula of inclusion, used by C. S. Peirce, Schröder, and others. De Morgan uses a copula defined as standing for any relation both transitive and convertible. The latter character consists in this, that whatever terms I and J may be, if we represent this copula by is in black-letter, then from ‘I is J’ it follows that ‘J is I.’ From these two propositions, we conclude, by Barbara, that ‘I is I.’ Such copulas are, for example, ‘equal to,’ and ‘of the same colour as.’ For any such copula there will be some relative term r, such that the proposition ‘S is P’ will be precisely equivalent to ‘S is r to everything, and only to everything, to which P is r.’ Such a copula may be called a copula of correlative identity. If the last proposition follows from the last but one, no matter what relative r may be, the copula is the copula of identity used by Thomson, Hamilton, Baynes, Jevons, and many others.
It has been demonstrated by Peirce that the copula of inclusion is logically simpler than that of identity.
Diagram: see LOGICAL DIAGRAM.
Dialogism. A form of reasoning in which from a single premise a disjunctive, or alternative, proposition is concluded introducing an additional term; opposed to a syllogism, in which from a copulative proposition a proposition is inferred from which a term is eliminated.
Syllogism.All men are animals, and all animals are mortal;
\ All men are mortal.Dialogism.Some men are not mortal;
\ Either some men are not animals, or some animals are not mortal.
Dimension. An element or respect of extension of a logical universe of such a nature that the same term which is individual in one such element of extension is not so in another. Thus, we may consider different persons as individual in one respect, while they may be divisible in respect to time, and in respect to different admissible hypothetical states of things, &c. This is to be widely distinguished from different universes, as, for example, of things and of characters, where any given individual belonging to one cannot belong to another. The conception of a multidimensional logical universe is one of the fecund conceptions which exact logic owes to O. H. Mitchell. Schröder, in his then second volume, where he is far below himself in many respects, pronounces this conception ‘untenable.’ But a doctrine which has, as a matter of fact, been held by Mitchell, Peirce, and others, on apparently cogent grounds, without meeting any attempt at refutation in about twenty years, may be regarded as being, for the present, at any rate, tenable enough to be held.
Dyadic relation. A fact relating to two individuals. Thus, the fact that A is similar to B, and the fact that A is a lover of B, and the fact that A and B are both men, are dyadic relations; while the fact that A gives B to C is a triadic relation. Every relation of one order of relativity may be regarded as a relative of another order of relativity if desired. Thus, man may be regarded as man coexistent with, and so as a relative expressing a dyadic relation, although for most purposes it will be regarded as a monad or non-relative term.
Index (in exact logic): see sub verbo.
Many other technical terms are to be found in the literature of exact logic.
Literature: for the study of exact logic in its more recent development, excluding probability, the one quite indispensable book is SCHRÖDER, Algebra d. Logik; and the bibliography therein contained is so exhaustive that it is unnecessary to mention here any publications previous to 1890. Schröder's pains to give credit in full measure, pressed down and running over, to every other student is hardly less remarkable than the system, completeness, and mathematical power of his work, which has been reviewed by C. S. PEIRCE in the Monist, vii. 19-40, 171-217. See also C. S. PEIRCE, Studies in Logic; Pop. Sci. Mo., xii. 1; and Proc. Amer. Acad. Arts and Sci., vii. 287. Cf. SCIENTIFIC METHOD. (C.S.P.)
Logical [Lat. logicalis, from logica, logic]: Ger. logisch; Fr. logique; Ital. logico. Irrespective of any facts except those of which logic needs to take cognizance, such as the facts of doubt, truth, falsity, &c.
Logical possibility is, according to usage, freedom from all contradiction, explicit or implicit; and any attempt to reform the inaccuracy would only bring confusion.
Logical necessity is the necessity of that whose contrary is not logically possible.
Logical induction is an induction based on examination of every individual of the class to which the examination relates. Thus, conclusions from a census are logical inductions. While this mode of inference is a degenerate form of induction, it also comes into the class of dilemmatic reasoning.
Logical truth is a phrase used in three senses, rendering it almost useless.
1. The harmony of a thought with itself. Most usually so defined, but seldom so employed. So far as this definition is distinct, it makes logical truth a synonym for logical possibility; but, no doubt, more is intended (Hamilton, Lects. on Logic, xxvii).
2. The conformity of a thought to the laws of logic; in particular, in a concept, consistency; in an inference, validity; in a proposition, agreement with assumptions. This would better be called mathematical truth, since mathematics is the only science which aims at nothing more (Kant, Krit. d. reinen Vernunft, 1st ed., 294).
3. More properly, the conformity of a proposition with the reality, so far as the proposition asserts anything about the reality. Opposed, on the one hand, to metaphysical truth, which is an affection of the ens, and on the other hand to ethical truth, which is telling what a witness believes to be true (Burgersdicius, Inst. Met., chap. xviii).
Logical parts and whole. Parts and whole of logical extension.
Logical reasoning. Reasoning in accordance with a LEADING PRINCIPLE (q.v.) which thorough analysis, discussion, and experience have shown must lead to the truth, in so far as it is relied upon. But what Aristotle understood by a logical demonstration may be seen in his De generatione animalium, Lib. II. cap. viii.
Logical presumption. A Wolffian term for synthetic reasoning, that is, induction and analogy; for hypothetic reasoning was not recognized as reasoning at all. The uniformity of nature is called the principle of logical presumption.
Logical division. Division into logical parts.
Logical distinctness. That distinctness which results from logical analysis.
Logical actuality. Kant, in the Logik by Jäsche (Einleitung, vii), defines logical actuality as conformity to the principle of sufficient reason, consisting of the cognition having reasons and having no false consequences; and he makes this, along with logical possibility, to constitute logical truth, which is thus used in its second sense. But in the Critic of the Pure Reason, in discussing the functions of judgments (1st ed., 75), he says that an assertoric proposition asserts logical actuality (Wirklichkeit, which Max Müller wrongly translates ‘reality’), and makes this phrase synonymous with logical truth (which is thus used in its third, and proper, sense).
Logical definition. A strict definition by genus and specific difference. Ockham and his followers objected to the designation on the ground that the logician, as such, had no occasion to define any ordinary term, such as man (Tractatus logices, Pt. I. chap. xxvi). (C.S.P.)
Logical Diagram (or Graph): Ger. logische Figur; Fr. diagramme logique; Ital. diagramma logico. A diagram composed of dots, lines, &c., in which logical relations are signified by such spatial relations that the necessary consequences of these logical relations are at the same time signified, or can, at least, be made evident by transforming the diagram in certain ways which conventional ‘rules’ permit.
In order to form a system of graphs which shall represent ordinary syllogisms, it is only necessary to find spatial relations analogous to the relations expressed by the copula of inclusion and its negative and to the relation of negation. Now all the formal properties of the copula of inclusion are involved in the principle of identity and the dictum de omni. That is, if r is the relation of the subject of a universal affirmative to its predicate, then, whatever terms X, Y Z may be,
Every X is r to an X; and if every X is r to a Y, and every Y is r to a Z, every X is r to a Z. Now, it is easily proved by the logic of relatives, that to say that a relation r is subject to these two rules, implies neither more nor less than to say that there is a relation l, such that, whatever individuals A and B may be,
If nothing is in the relation l to A without being also in the same relation l to B, then A is in the relation r to B; and conversely, that,
If A is r to B, there is nothing that is l to A except what is l to B.
Consequently, in order to construct such a system of graphs, we must find some spatial relation by which it shall appear plain to the eye whether or not there is anything that is in that relation to one thing without being in that relation to the other. The popular Euler's diagrams fulfil one-half of this condition well by representing A as an oval inside the oval B. Then, l is the relation of being included within; and it is plain that nothing can be inside of A without being inside B. The relation of the copula is thus represented by the spatial relation of ‘enclosing only what is enclosed by.’ In order to represent the negation of the copula of inclusion (which, unlike that copula, asserts the existence of its subject), a dot may be drawn to represent some existing individual. In this case the subject and predicate ovals must be drawn to intersect each other, in order to avoid asserting too much. If an oval already exists cutting the space in which the dot is to be placed, the latter should be put on the line of that oval, to show that it is doubtful on which side it belongs; or, if an oval is to be drawn through the space where a dot is, it should be drawn though the dot; and it should further be remembered that if two dots lie on the boundaries of one compartment, there is nothing to prevent their being identical. The relation of negation here appears as ‘entirely outside of.’ For a later practical improvement see Venn, Symbolic Logic, chap. xi. (C.S.P.)
Logomachy [Gr., taken from the First Epistle of Paul to Timothy, vi. 4 νοσῶν περὶ ζητήσεις καὶ λογομαχίας, doting about questions and strifes of words]: Ger. Logomachie, Wortstreitigkeit; Fr. logomachie; Ital. contesa di parole. A contention (in which it is not essential that two parties should be active) not professedly relating to the use of words and phrases, but in which proper care exercised to make the ideas clear will show the critic, either that there is no important difference between the position attacked and that defended, or if there is, that the argumentation does not relate to such points.
Theology and subjects connected with it, such as the freedom of the will, have been the great theatre of such war. At present it is still kept up in logic; and other branches of philosophy are not entirely freed from it. Disputes about the propriety of modes of speech, however hot and silly they may be, are not logomachy. (C.S.P.)
Major and Minor (extreme, term, premise, satz, &c., in logic): Ger. Ober- and Unter- (Begriff, &c.); Fr. majeur and mineur; Ital. maggiore and minore. The subject and predicate of the conclusion of a syllogism are called the extremes (τα ἀκρα, by Aristotle), because they are only brought together by the agency of the third term, called, on that account, the middle term (ὁ μεσος ὁρος, Aristotle). Of the two extremes, the one that is the predicate of the conclusion is called the major extreme (το μειζον ἀκρον, Aristotle), because in a universal affirmative proposition (the typical formal proposition) its breadth is the greater, while the subject of the conclusion is the minor extreme (το ἐλαττον ἀκρον, Aristotle).
Whether the expressions major term and minor term, for the major and minor extremes, are grammatically accurate or not, they are consecrated by usage through the scholastic period. The major and minor premises are respectively those which contain the major and minor extremes. Aristotle (I. Anal. Pr., ix) calls the former ἡ προς το μειζον ἀκρον προτασις, ‘the proposition about the major extreme.’ (C.S.P.)
Mark [AS. mearc, a bound]: Ger. Merkmal; Fr. marque, attribut; Ital. segno (contrassegno), nota. To say that a term or thing has a mark is to say that of whatever it can be predicated something else (the mark) can be predicated; and to say that two terms or things have the same mark is simply to say that one term (the mark) can be predicated of whatever either of these terms or things can be predicated.
The word translates the Latin nota. It has many practical synonyms, such as quality, mode, attribute, predicate, character, property, determination, consequent, sign. Most of these words are sometimes used in special senses; and even when they are used in a general sense, they may suggest somewhat different points of view from mark. (C.S.P., C.L.F.)
A great oversight which had vitiated the entire discourse of logicians about marks, and had prevented them from fully understanding what marks are, was corrected by Augustus de Morgan when he observed that any collection whatever of individuals has some mark common and peculiar to them. That it is so will appear when we consider that nothing prevents a list of all the things in that collection from being drawn up. Now, the mere being upon that list, although it has not actually been drawn up, constitutes a common and peculiar mark of those individuals. Of course, if anybody tries to specify a number of individuals that have no common and peculiar mark, this very specification confers upon their common and peculiar mark a new degree of actuality.
On the other hand, if two marks are common and peculiar to precisely the same collection of things, they may, for the ordinary purposes of formal logic, be looked upon as the same mark. For it is indifferent to formal logic how objects are marked, whether in a simpler or more complex way. We may, therefore, regard the two marks as constituting together a single mark. Marks, after all, are not the object of logical study; they are only fictitious aids to thought. (C.S.P.)
Material Fallacy. This term originated with Whately (Encyc. Metropolitana, i. 218 b). Whately's material fallacies are those in which the conclusion does follow from the premises. Therefore, excluding the multiple interrogation, which is no syllogism, of the rest of Aristotle's thirteen, only the ignoratio elenchi and the petitio principii are material. Cf. FALLACY (also for foreign equivalents).
Aldrich had modified Aristotle's division into fallacies in dictione and fallacies extra dictionem; making a division into Sophismata in forma argumenti (sicubi conclusio non legitime consequatur ex praemissis), and Sophismata in materia argumenti (sicubi legitime non tamen vere concludere videatur syllogismus). Under the latter head he placed the ignoratio elenchi, the non causa pro causa, the non sequitur, and the petitio principii. Whately's distinction is—whether from a theoretical or a practical point of view—by far the most important that can be drawn among fallacies; so that besides the reason of priority, which ought itself to be final, the needs of the logician forbid us to depart from Whately's definition. Some logicians do not admit material fallacies among the number of fallacies, but consider them to be faults of method (Hamilton, Lects. on Logic, xxvi; Ueberweg, Syst. d. Logik, §§ 126, 137). E.E. Constance Jones (Elements of Logic as a Science of Propositions, § xxvi) reduces them to formal fallacies. Hyslop (Elements of Logic, chap. xvii) uses the term material fallacy, quite unjustifiably, to include all fallacies due to something in the matter of reasoning. (C.S.P.)
Material Logic: Ger. materielle Logik; Fr. logique matérielle; Ital. logica materiale. Formal logic classifies arguments by producing forms in which, the letters of the alphabet being replaced by any terms whatever, the result will be a valid, probable, or sophistic argument, as the case may be; material logic is a logic which does not produce such perfectly general forms, but considers a logical universe having peculiar properties.
Such, for example, would be a logic in which every class was assumed to consist of a finite number of individuals; so that the syllogism of transposed quantity would hold good. In most cases material logic is practically a synonym of applied logic. But a system like Hegel's may also properly be termed material logic. The term originated among the English Occamists of the 14th century, who declared Aristotle's logic to be material, in that it did not hold good of the doctrine of the Trinity. (C.S.P.)
Mathematical Logic: Ger. (1) Logik der Mathematik; Fr. (1) logique des mathématiques; Ital. (1) logica della matematica. (1) The logical analysis of mathematics. (C.S.P.)
(2) SYMBOLIC LOGIC (q.v.).
Literature (to 1): the logic of arithmetic is treated by DEDEKIND in his Was sind und was sollen die Zahlen? (Eng. trans. in Essays on Number, 1901). See also the ninth lecture of the third volume of SCHRÖDER, Logik; and FINE, Number System of Algebra. For the logic of the calculus, see the second edition of JORDAN, Cours d'Analyse; also CLIFFORD, Theory of Metrics, in his Mathematical Papers; WEBER, Algebra; and the papers of G. CANTOR, some of which are contained in the Acta Mathematica, ii, and subsequent ones in the Mathematische Annalen, 15, 17, 20, 21, 23, 46, 49. LISTING'S papers on topical geometry are two, one in the Gött. Abhand., the other in the Gött. Nachr. Several of RIEMANN'S papers are valuable in a logical point of view. See also CAUCHY, Théorie des Clefs. PETERSEN, Methods and Theories, shows how to solve problems in elementary geometry. Cf. MATHEMATICS. (C.S.P.)
Matter and Form: Ger. Materie (Stoff) und Form; Fr. la matière et la forme; Ital. materia e forma. The word matter (Lat. materia, which was used to translate the Gr. ὑλη) is often employed where the more appropriate Greek word would be σωμα, corpus, body; or το ὑποκειμενον, subjectum, or even ἡ ὑποστασις, translated person in theology. Form (Lat. forma, used to translate the Gr. μορφη and εἰδος, though the latter is more exactly represented by species) is often employed where σχημα, figure, or τυπος, shape, would be near equivalents. The Greek expressions μορφη, παραδειγμα, εἰδος, ἰδεα, το τι εστι, το τι ἠν εἰναι are pretty nearly synonymous.
The distinction of matter and form was first made, apparently, by Aristotle. It almost involves his metaphysical doctrine; and as long as his reign lasted, it was dominant. Afterwards it was in disfavour; but Kant applied the terms, as he did many others drawn from the same source, to an analogous but widely different distinction. In many special phrases the Aristotelian and Kantian senses almost coalesce, in others they are quite disconnected. It will, therefore, be convenient to consider: (1) the Aristotelian distinction; (2) the Kantian distinction; and (3) special applications.
The Aristotelian distinction. Not only was the distinction originated by Aristotle, but one of the two conceptions, that of matter, is largely due to him. Indeed, it is perhaps true that the Greek word for matter in the sense of material, ὑλη, was never understood in that general sense before Aristotle came to Athens. For the first unquestionable cases of that meaning occur in certain dialogues of Plato, concerning which—though there are no dates that are not open to dispute—it seems to the present writer that it is as certain as any such fact in the history of Greek philosophy that the earliest of them was written about the time of Aristotle's arrival. It is true that, as Aristotle himself says, matter was the earliest philosophical conception. For the first Ionian philosophers directed their thoughts to the question what the world was made of. But the extreme vagueness of the notion with them is shown by their calling it ἡ ἀρχη, the beginning, by the nonsense of the question, and by many more special symptoms. If the philosophical conception of matter distinguished the metaphysics of Aristotle, that of Plato had been no less marked by its extraordinary development of the notion of form, to which the mixed morality and questioning spirit of Socrates had naturally led up; the morality, because the form is the complex of characters that a thing ought to have; the questioning, because it drew attention to the difference between those elements of truth which experience brutally forces upon us, and those of which reason persuades us, which latter make up the form. But Aristotle's distinction set form, as well as matter, in a new light.
It must not be forgotten that Aristotle was an Asclepiad, that is, that he belonged to a family which for generation after generation, from prehistoric times, had had their attention turned to vital phenomena; and he is almost as remarkable for his capacity as a naturalist as he is for his incapacity in physics and mathematics. He must have had prominently before his mind the fact that all eggs are very much alike, and all seeds are very much alike, while the animals that grow out of the one, the plants that grow out of the other, are as different as possible. Accordingly, his dunamis is germinal being, not amounting to existence; while his entelechy is the perfect thing that ought to grow out of that germ. Matter, which he associates with stuff, timber, metal, is that undifferentiated element of a thing which it must possess to have even germinal being. Since matter is, in itself, indeterminate, it is also in itself unknowable; but it is both determinable by form and knowable, even sensible, through form. The notion that the form can antecede matter is, to Aristotle, perfectly ridiculous. It is the result of the development of matter. He looks upon the problem from the point of view of a naturalist. In particular, the soul is an outgrowth of the body.
The scholastics, who regarded Aristotle as all but infallible, yet to whom the ideas of a naturalist were utterly foreign, who were thoroughly theological in their notions, admitted that the soul was a form. But then, they had great difficulty with those opinions of their master which depended upon his conceiving of matter as more primitive than form. Their notions of form were rather allied to those of Plato. The mode of being that, in some sense, anteceded individual existence, they would have held to be one in which there was form without matter, if awe of Aristotle had not caused them to modify the proposition in one way or another. A question, for example, which exercised them greatly was, how the form was restricted to individual existence? For Aristotle there could not be any such question, because he did not conceive of a form taking on individuality, but of an undifferentiated matter taking on, or rather developing, form, and individuality, perhaps, with it (412 a, 7).
The Kantian distinction. Aristotle refuses to consider any proposition as science which is not universal. He does not go so far as to say that all knowledge involves synthesis, but he often approaches doing so. In particular, he holds that matter is something in itself beyond our knowledge, but the existence of which has to be assumed in order to synthetize the opposites that are involved in all change. He expressly defines that as the function of the conception of matter. With Kant, the view that all knowledge involves synthesis—various acts of synthesis one over another—is vastly more developed; and he, too, employs the terms matter and form as called for by such synthesis. But it is curious that while with Aristotle it is matter that is the quasi-hypothesis imported into the facts that the mind may synthetize, with Kant, on the other hand, it is form which performs this function. The matter of cognition consists of those elements which are brutally and severally forced upon us by experience. By the form he means the rational or intelligible elements of cognition, which he wishes, as far as possible, to regard as independent contributions of the mind itself, which we have no right to suppose are duplicated by anything corresponding to them in the thing. For the Aristotelian, all pure matter is exactly alike, equally devoid of all predicates, while the forms make all the variety of the universe. For the Kantian, on the other hand, matter is the manifold, while the pure forms are the few different modes of unity. Nevertheless, the Kantians—indeed, Kant himself (see the Critic of the Pure Reason, 1st ed., 266)—argued that they were using the terms in their old and accepted sense. What enabled them to give some speciousness to their contention was the circumstance that during the full century and more of neglect of the Aristotelian doctrine that had intervened, certain secondary senses of the term matter, especially that of corporeal matter, and that of a species of corporeal matter, had become relatively prominent.
Special senses. Although there is only one first or primary matter, absolutely indeterminate, yet Aristotle often uses the term in a modified sense as that which is relatively indeterminate; so that the last or second matter is the same as the form. But these phrases are also used in quite other senses, which need not here be specially noticed. Matter being taken relatively, the same thing can have this or that as its matter in different respects; and so matter is distinguished into materia ex qua, in qua, and circa quam. Materia ex qua is the material; silver is the materia ex qua of a dime. Materia in qua is the subject in which the form inheres; materia circa quam is the object. Aquinas illustrates the distinction by virtue, which is a form, and, as such, has no materia ex qua; but it has a subject in which it inheres and an object upon which it is exercised. Aquinas introduced the term signate matter. Matter of composition, or proximate matter, is that of which a thing consists; matter of generation, or remote matter, that from which it is developed, as a seed or egg.
The varieties of form are so numerous that they may best be taken in alphabetical order.
Absolute form: form abstracted from matter.
Accidental form: an accident, or that the presence of which constitutes an accident; as music is the accidental form of the musician.
Advenient form: a form subsequent to the final form.
Apprehended form = apprehended SPECIES (q.v.).
Artificial form: a form superinduced by art.
Assistant form: an agent aiding in the realization of a form, especially of that whose essential character is to move; as the angel who turns the heavens round once every twenty-four hours, or the captain of a ship.
Astral form. According to Gilbert (De Magnete), phenomena of electricity are produced by a material effluvium, while the action of a magnet takes place directly at a distance. Whatever it may be then which constitutes the magnetic field, not being matter, must be called form. Gilbert names it forma prima radicalis et astralis.
Common form: a form belonging to a species.
Completive form: used by Aquinas in the sense of the last of the series of forms which gradually bring a thing to fully developed existence. By Aristotle called last form.
Composite form: the form of a collective whole, so far as it is different from its parts.
Corporeal form: a form of a corporeal nature. This is used by Aquinas, Summa Theol., pars I. qu. 1xv. art. 4. See Material form.
Disponent form: a form rendering matter apt to receive another, principal, form. Thus, dryness in wood disposes it to receive combustibility.
Elementary form: one of the four combinations of hot and cold with moist and dry which were supposed to characterize the four elements.
Exemplar form: an idea.
Final form: see Completive form.
General form: the form of a genus; as we should now say a generic form.
Immaterial form: a form which neither depends upon matter while it is being made nor after it is made; a term employed in the theological doctrine of creation.
Incorruptible form: a form not subject to corruption.
Individual form: in one of the theories of individuation, was a form which by existing in matter acquired the power of individuating another form.
Informant form: a form which is a part of the thing of which it is the form.
Inherent form: a form which can only exist in a state of inherence in matter.
Intellective form: the mind as form.
Intelligible form: see Sensible form.
Intermediate form: a form having a middle position between an elementary and a completive form.
Material form: a term of Scotus, who defines it as follows: ‘Formam materialem dico esse omnem illam, quae ex natura sua necessario inclinatur naturaliter, ut sit actus materiae, sive sit substantialis, sive accidentalis’ (Op. Oxon., IV. i. 1); ‘Ideo dici potest tertio modo.’ But elsewhere (ibid., 1 Post. qu. ii.) he distinguishes two senses of the term: ‘Forma materialis potest intelligi dupliciter. Uno modo dicitur, quae educitur de potentia materiae, vel quia utitur organo corporeo in operando: et isto modo forma intellectiva non est forma materialis. Alio modo dicitur forma materialis, quia perfectio materiae, et isto modo anima intellectiva est forma materialis, ideo aliquam variationem potest accipere a materia, quam perficit, quia ex materia et forma fit vere unum.’ Perhaps the most accessible book from which to gain a hint of the nature of the difficulty which gives rise to this distinction is Bridges' edition of what is called The Opus Majus of Roger Bacon, ii. 507-11, cap. ii.
Mathematical form: an object of mathematical contemplation, and the result of mathematical abstraction.
Metaphysical form: form in the philosophical sense.
Native or natural form, forma in natura exsistens, forma naturae, form of a nature, is a term going back to John of Salisbury (Opera, ed. Giles, v. 92), and closely connected, if not synonymous, with material form. Certain questions started by Aristotle in Book V of the Metaphysics (of which there is an admirable periphrastic translation by Grote, Aristotle, 2nd ed., 619 ff.) gave rise to discussions in which the doctrine was compared with Christian beliefs; and the natural form plays a considerable part in such discussions.
Bacon adopted the term forma naturae. He did not grossly depart from the received meaning of the term, but owing to his occupying himself with inquiries quite antipodal to those of the scholastics, the two parties did not understand one another. Bacon means the physical explanation of a phenomenon, its occult modus operandi. Among the followers of Bacon we, at first, hear a great deal about forms. Boyle wrote whole books about them. But the distinction of matter and form was not calculated to further such inquiries as theirs. It is adapted to expressing phenomena of life. It might be twisted to such a purpose as Gilbert put it to (see Astral form), but it was not suited to the mechanical philosophy of Boyle, and only led to wordy and fruitless discussions.
Participate form: a form considered as it is united with matter.
Preparatory form: a term used by Boyle where disponent form would be more technical. He says, ‘The preparatory form is but (if I may so speak) a harbinger that disposes the matter to receive a more perfect form, which, if it be not to be succeeded by any other more noble, is entitled the specific form of that body; as in the embryo, the vegetative and the sensitive soul is but preparatory to the rational, which alone is said to be the specific form of man’ (Free Considerations about Subordinate Forms).
Physical form: such forms as may form the object of physical inquiries. Of course, the term was very differently understood during scholastic times and in the 17th century. But the above definition covers both uses.
Primary form. There is no such well-recognized term of metaphysics; but a remark of William Gilbert leads us to suppose that medical men attached some meaning to it.
Principal form is that which per se constitutes a species. Called also specific form.
Radical form: see Astral form.
Sensible form. Though it chances that Aristotle nowhere distinguishes μορφη into αἰσθητη and νοητη, yet his followers did. Sensible forms are those which the outward senses distinguish; intelligible are those which the intellect alone can distinguish.
Significate form: a Thomistic term, a form distinguished by a name.
Simple form: form without matter. ‘Forma simplex, quae est purus actus, est solus deus,’ says St. Thomas.
Specific form: see Principal form.
Subsistent form: a form capable of existing separate from matter, as Aquinas holds that the angels and departed spirits are.
Substantial form: a form which constitutes a nature, i.e. a species or genus. Thus, the accidental form of a musician is music; but his substantial form is the rational soul which makes him a man. When men's thoughts became turned from theology to the investigation of physics, those who were animated by the new spirit found themselves confronted with objections based upon allegations of substantial forms. That these substantial forms, so used, were merely a hindrance to the progress of science, was quite plain to them. But the objections were urged with a logical accuracy, born of centuries of study, with which the new men were utterly incapable of coping. Their proper course would have been quietly to pursue their own inquiries, and leave the theologians to square their results with philosophy as best they could. But circumstances did not permit this. The theologians had the popular intelligence and the arm of power on their side; and when an apparent opposition arose, they naturally exerted themselves to put it down. Thus, the innovators were led to protest against these senseless and harmful substantial forms; and they had to formulate their objections to them—a business for which they were entirely unfitted. But since the discoveries of the physicists were plainly adding to man's knowledge and power, while their antagonists were simply obstructive, the former soon carried the day in the general opinion of mankind. The history proves that there was something vicious about the theological application of substantial forms; but it in no degree goes to show that the physicists accurately defined the objection to that application. In reviewing the arguments at the present day, when the position of the mechanical philosophers is becoming almost as obsolete as that of the scholastic doctors, we first note that when the new men denied that the substantial forms were ‘entities,’ what they really had in mind was, that those forms had not such a mode of being as would confer upon them the power dynamical to react upon things. The Scotists, for it was they upon whom, as being in possession of the universities, the brunt of the battle fell, had in fact never called the substantial forms ‘entities,‘ a word sounding like a Scotistic term, but in fact the mere caricature of such a term. But had they used the word, nothing more innocent than the only meaning it could bear for them could be imagined. To call a form an ‘entity’ could hardly mean more than to call it an abstraction. If the distinction of matter and form could have any value at all, it was the substantial forms that were, properly speaking, forms. If the Scotists could really specify any natural class, say man—and physics was at that time in no condition to raise any just doubt upon that score—then they were perfectly justified in giving a name to the intelligible characteristic of that class, and that was all the substantial form made any pretension to being. But the Scotists were guilty of two faults. The first—great enough, certainly, but relatively inconsiderable—was often referred to, though not distinctly analysed and brought home to them. It was that they were utterly uncritical in accepting classes as natural, and seemed to think that ordinary language was a sufficient guarantee in the matter. Their other and principal fault, which may with justice be called a sin, since it involved a certain moral delinquency, was that they set up their idle logical distinctions as precluding all physical inquiry. The physicists and Scotists, being intent upon widely discrepant purposes, could not understand one another. There was a tolerably good excuse for the physicist, since the intention of the Scotist was of an abstract and technical kind, not easily understood. But there was no other excuse for the Scotist than that he was so drugged with his metaphysics that ordinary human needs had lost all appeal to him. All through the 18th century and a large part of the 19th, exclamations against the monstrousness of the scholastic dogma that substantial forms were entities continued to be part of the stock-in-trade of metaphysicians, and it accorded with the prevalent nominalism. But nowadays, when it is clearly seen that physical science gives its assent much more to scholastic realism (limited closely to its formal statement) than it does to nominalism, a view of the history more like that here put forward is beginning to prevail.
In the following terms, mostly Kantian, prepositional phrases express the qualifications.
Form of corporeity: a very common term of scholasticism, originating with Avicenna, and used by Aquinas (Summa Theol., pars i. cap. 1xvi. art. 2), but more particularly by Scotus (in his great discussion Opus Oxon., IV. dist. xi. 9. 3, beginning ‘De secundo articulo dico’) and by all his followers. The point is, that the rational soul, being purely spiritual, cannot confer corporeity upon the human body, but a special form, the form of corporeity, is requisite. Suarez and others, generally Thomists, as well as Henry of Ghent, denied this on the ground that a species has but one form. Thus a great metaphysical dispute arose. It sprung from the study of the doctrine of transubstantiation. See Cavellus, Suppl. ad quaest. Scoti in De Anima, disp. i, which is in the Lyons ed. of Scotus, tom. ii.
Form of cognition, in Kant's doctrine, is that element of knowledge which the matter of experience must assume in order to be apprehended by the mind. Kant seems to have been thinking of legal forms which must be complied with in order to give standing before a court. So an English sovereign, in order to be crowned, must, as a ‘matter of form,’ swear to an intensity of loathing for Romish dogmas which he probably regards with great coolness. Kant's definitions are chiefly the following:—
‘In the phenomenon, that which corresponds to the impression of sense, I call the matter of it; while that which constitutes the fact that manifoldness of the phenomenon is intuited as ordered in certain relations, I call the form of the phenomenon’ (Krit. d. reinen Vernunft, 1st ed., 20).
‘All cognition requires a concept, be it as imperfect and dark as you will; and this, in respect to its form, is always a universal which serves as a rule’ (ibid., 106).
‘The transcendental unity of the synthesis of the imagination is the pure form of all possible cognition, through which, consequently, all objects of possible experience must a priori be represented’ (ibid., 118).
‘There are two factors in cognition; first, the concept by which any object is thought—that is, the category; and secondly, the intuition by which that object is given. For if the concept had had no corresponding intuition, it would be a thought, no doubt, as far as its form goes; but having no object, no cognition whatsoever [he means, whether true or false] of anything would be possible by it; since, so far as I should know, there would be nothing, and perhaps could be nothing, to which such a concept would be applicable’ (2nd ed. of the Deduction of the Categories, § 22).
‘It is not more surprising that the laws of phenomena in nature must agree with the understanding and its a priori form, i.e. with its power of combining any manifold, than that the phenomena themselves must agree with the a priori form of sensuous intuition. For just as phenomena have no existence in themselves, but are merely relative to the mind, as having senses, so laws do not exist in the phenomena, but are merely relative to the mind in which the phenomena inhere, that mind exercising understanding’ (and see the rest of this passage, ibid., § 26).
Form of forms. Francis Bacon says ‘the soul may be called the form of forms,’ which would be a pretty conceit, were it not plagiarized from the serious doctrine of Aristotle: ὁ νους εἰδος εἰδων (432 a, 2).
The terms matter and form are used in certain peculiar ways in logic. Speaking materialiter, the matter of a proposition is said to be its subject and predicate, while the copula is its form. But speaking formaliter, the matter of a proposition is, as we familiarly say, the ‘matter of fact’ to which the proposition relates; or as defined by the scholastics, ‘habitudo extremorum adinvicem.’ The second tractate of the Summulae of Petrus Hispanus begins with the words: ‘Propositionum triplex est materia; scilicet, naturalis, contingens, et remota. Naturalis est illa in qua praedicatum essentia subiecti vel proprium eius; ut, homo est animal; vel, homo est risibilis. Contingens est illa in qua praedicatum potest adesse et abesse subiecto praeter subiecti corruptionem; ut, homo est albus, homo non est albus. Remota est illa in qua praedicatum non potest convenire cum subiecto; ut, homo est asinus.’
Of a syllogism, the proximate matter is the three propositions; the remote, the three terms. The form, which ought to be the ergo, by the same right by which the copula is recognized as the form of the proposition, is said to be ‘apta trium propositionum dispositio ad conclusionem ex praemissis necessario colligendam.’ But Kant, in the Logik by Jäsche, § 59, makes the premises the matter, and the conclusion the form. (C.S.P.)
Maxim (in logic). A widely received general assertion or rule.
The earliest writers, so far as has been shown, to use maxima as a substantive were Albertus Magnus and Petrus Hispanus. The former (Post. Anal., lib. I. cap. ii) makes maximae constitute the seventh of thirteen classes of propositions which may be accepted, though they are uncertain, so that they differ widely from dignitates, or axioms. He says, ‘Maximae propositiones opinantur esse quae non recipiuntur nisi in quantum sunt manifestae. Et putat vulgus commune et alii simplices et non periti quod sint primae ex sui veritate communicantes omnem intellectum; sicut est ista propositio, Mendacium est turpe,’ &c. Hamilton quotes, but gives an unverifiable reference to, a sentence in which Albertus makes maxima another name for a dignitas. Petrus Hispanus (Summulae, v) says, ‘Maxima est propositio qua non est altera prior neque notior’; and he divides commonplace into two kinds, called Maxim and Difference of Maxim. This phraseology was so generally followed that it is surprising that Prantl's attribution of it to Albert of Saxony (who simply copies the Summulae here, almost verbatim) should have found any acceptance. Blundevile and other early writers of logic in English take the word from the Summulae. It was also adopted into English law. The meaning now tends to return to that used by Albertus. Kant (Krit. d. reinen Vernunft, 1st ed., 666) defines a maxim of reason as a subjective principle derived not from the character of the object, but from the interest of reason in such perfection of cognition as may be possible; and in the Critic of the Practical Reason he endeavours to make out something analogous in that sphere. In the Logik by Jäsche (Einleitung III) he defines a maxim as an inward principle of choice between different ends. (C.S.P.)
Method and Methodology, or Methodeutic: Ger. Methodenlehre; Fr. méthodologie, théorie de la méthode; Ital. teoria dei metodi, metodologia. A branch of logic which teaches the general principles which ought to guide an inquiry.
Owing to general causes, logic always must be far behind the practice of leading minds. Moreover, for the last three centuries thought has been conducted in laboratories, in the field, or otherwise in the face of the facts, while chairs of logic have been filled by men who breathe the atmosphere of the seminary. The consequence is that we can appeal to few works as showing what methodology ought to be. The first book of Bacon's Novum Organum is well enough, as far as it goes, and was no doubt useful in its day. Senebier's L'Art d'observer is instructive. Comte's Philosophie positive accomplished something. Whewell's History of the Inductive Sciences and other works have the advantage of being written by a man of great power of investigation himself, who drew his doctrine from the facts of scientific history. Mill's System of Logic is, no doubt, of considerable value, although the author knew too little of science. There is hardly one of the illustrations of fine method adduced in his first edition which has not been refuted. Beneke's Logik in praktischer Absicht was not altogether without value. Of great value, also, is Jevon's Principles of Science. Pearson's Grammar of Science is a work of great force, but unfortunately too much influenced by certain philosophical ideas. Wundt devotes two of the three volumes of his Logik to Methodenlehre.
The traditional doctrine of method is confined chiefly to rules of definition and division, which teach an exactness of thought much needed, but are marked by the total absence of modern ideas. Cf. SCIENTIFIC METHOD, and EVIDENCE. (C.S.P.)
Middle Term (and Middle) [trans. of terminus medius, medium, used by Boethius to translate Aristotle's ὁ μεσος ὁρος, το μεσον]: Ger. Mittelbegriff; Fr. terme moyen; Ital. mezzo termine, termine medio. The adjective μεσον is applied in Greek to a third object additional to two others, when the idea of intervening can hardly be detected. It is, therefore, perhaps needless to seek further for Aristotle's intention in calling that term, by the consideration of which two others are illatively brought into one proposition as its subject and predicate, the middle term, or middle. It is the most important factor of Aristotle's theory of reasoning.
The same word means little more than third in the phrase ‘principle of excluded middle,’ which is, indeed, often called principium exclusi tertii. See LAWS OF THOUGHT. On the other hand, something which partakes of each of two disparate natures, and renders them capable of influencing one another, is called a tertium quid (Aristotle's ἡ τριτη οὐσια). (C.S.P., C.L.F.)
Mixed [Lat. mixtum, from miscere, to mix]: Ger. vermischt; Fr. composé; Ital. misto. (1) Mixed proof: a proof which is partly analytic, partly synthetic.
(2) Mixed mode: a mode compounded of simple ideas of several kinds, put together to make one complex one (Locke, Essay concerning Human Understanding, Bk. II. chap. xii. § 5). See MODE.
(3) Mixed power: a power at once active and passive, because the principle of change is in itself. (C.S.P.)
Mnemonic Verses and Words (in logic). Aids to memory in logic, of the sort described under MNEMONICS (q.v.). (J.M.B.)
1. Instrumenta novem sunt, guttur, lingua, palatum. Quattuor et dentes, et duo labra simul.
The following mnemonic verses are contained in the Summulae Logicales of Petrus Hispanus, but were older, perhaps very much older.
2. ‘Quae?’ ca. vel hyp., ‘Qualis?’ ne. vel aff., u. ‘Quanta?’ univ. par. in. vel sing. [What is the substance of a proposition? categorical or hypothetical. What is its quality? negative or affirmative. What is its quantity? universal, particular, indefinite, or singular.]
3. Simpliciter Feci, convertitur Eva, per acci, A sto per contra: sic fit conversio tota. Asserit A, negat E, sed universaliter ambae; Asserit I, negat O, sed particulariter ambo.
[E and I are converted simply; E and A, per accidens; A and O, per contrapositionem.]
4. Prae, contradic.; post, contra.; prae postque, subalter.
Non omnis, quidam non; omnis non, quasi nullus;
Non nullus, quidam; sed ‘nullus non’ valet ‘omnis’;
Non aliquis, nullus; ‘non quidam non’ valet ‘omnis’;
Non alter, neuter; ‘neuter non’ praestat ‘uterque.’
[Non placed before omnis or nullus gives the contradictory proposition; placed after, the contrary; both before and after, the subalternate.]
5. Primus, Amabimus; Edentuli que, secundus;
Tertius, Illiace; Purpurea, reliquus.
Destruit u totum, sed a confirmat utrumque;
Destruit e dictum, destruit i que modum.
Omne necessariat; impossible, quasi nullus;
Possible, quidam; quidam non, possibile non.
E dictum negat, i que modum, nihil a, sed u totum.
[The first syllable of each of the four vocables Amabimus, Edentuli, Illiace, Purpurea, is for the possible mode; the second for the contingent; the third for the impossible; the fourth for the necessary. The vowel a signifies that both mode And ‘dictum’ are to be taken assertorically; e, that the dictum is to be denied; i, that the mode is to be denied; u, that both mode and dictum are to be denied. Each word refers to a line or order of equipollent modal forms.]
6. Tertus est quarto semper contrarius ordo.
Sit tibi linea subcontraria prima secundae.
Tertius est primo contradictorius ordo.
Pugnat cum quarto contradicendo secundus.
Prima subest quartae vice particularis habens se.
Hanc habet ad seriem se lege secunda sequentem.
[The relation of ‘Sortem impossible est currere’ and ‘Sortem necesse est currere’ is that of contraries; they cannot be true at once. The relation ‘Sortem possibile est currere’ and ‘Sortem possible est non currere’ is that of subcontraries; they cannot be false at once. The relation of ‘Sortem possibile est currere’ and ‘Sortem impossibile est currere’ is that of contradictories. The relation of ‘Sortem possibile est non currere’ and ‘Sortem necesse est currere,’ is likewise that of contradictories. ‘Sortem possibile est currere’ follows from ‘Sortem necesse est currere,’ as does ‘Sortem possibile est non currere’ from ‘Sortem impossibile est currere.’]
7. Sub. prae. prima, secunda prae. bis, tertia sub. bis.
[The first figure contains the middle term as subject and predicate; the second, the middle as predicated twice; the third, the middle twice as subject.]
8. Barbara, Celarent, Darii, Ferio, Baralipton,
Celantes, Dabitis, Fapesmo, Frisesomorum.
Cesare, Camestres, Festino, Baroko, Darapti,
Felapton, Disamis, Datisi, Bokardo, Ferison.
[These are original names of the syllogistic moods, which there is no sufficient reason for abandoning. The direct moods of the first figure are recognizable by their containing no sign of conversion, s, p, or k; the indirect moods (or moods of the fourth figure) by their having those signs attached either to the third vowel or to the first two. In the second figure, one of the signs s, p is attached to the first vowel, or to the second and third, or k is attached to the second. In the names of the moods of the third figure, s or p is attached to the second vowel, or to the first and third, or k to the first. There are also names for syllogism with weakened conclusions or strengthened premises, as well as for indirect moods of the first figure considered as belonging to a fourth. But the above rules will enable a reader to identify them. Thus, Bramantip can be nothing but Baralipton; while Barbari is Barbara with a weakened conclusion. Camenes can be nothing but Celantes; Dimaris nothing but Dabitis; Fesapo nothing but Fapesmo; Fresison nothing but Frisesomorum. A writer who introduces an m into the name of a mood containing an s or p only after its third vowel, or who omits m from the name of a mood having s or p after the first and second vowels, uses the fourth figure.]
9. Simpliciter vult s, verti p vero per acci. M vult transponi, k per impossibile duci.
Servat maiorem variatque secunda minorem;
Tertia maiorem variat servatque minorem.
[s, in the name of a mood, shows that the proposition denoted by the preceding vowel is, in a preferred mode of reduction, to be converted simply; p, that it is to be converted per accidens; m shows that the premises are to be transposed; k, that the preferred reduction is by reduction of the contradictory of the conclusion to an absurdity, this contradictory of the conclusion being, in the second figure, put in place of the minor premise (the major being retained), and in the third figure in the place of the major (the minor being retained).]
A great number of other memorial words and verses have been proposed by logicians. (C.S.P.)
Modality [Lat. modus; see MODE]: Ger. Modalität; Fr. modalité; Ital. modalità. There is no agreement among logicians as to what modality consists in; but it is the logical qualification of a proposition or its copula, or the corresponding qualification of a fact or its form, in the ways expressed by the modes possibile, impossibile, contingens, necessarium.
Any qualification of a predication is a mode; and Hamilton says (Lects. on Logic, xiv) that ‘all logicians’ call any proposition affected by a mode a modal proposition. This, however, is going much too far; for not only has the term usually been restricted in practice, from the age of Abelard, when it first appeared, until now, to propositions qualified by the four modes ‘possible,’ ‘impossible,’ ‘necessary,’ and ‘contingent,’ with only occasional extension to any others, but positive testimonies to that effect might be cited in abundance.
The simplest account of modality is the scholastic, according to which the necessary (or impossible) proposition is a sort of universal proposition; the possible (or contingent, in the sense of not necessary) proposition, a sort of particular proposition. That is, to assert ‘A must be true’ is to assert not only that A is true, but that all propositions analogous to A are true; and to assert ‘A may be true’ is to assert only that some proposition analogous to A is true. If it be asked what is here meant by analogous propositions, the answer is—all those of a certain class which the conveniences of reasoning establish. Or we may say the propositions which in some conceivable state of ignorance would be indistinguishable from A. Error is to be put out of the question; only ignorance is to be considered. This ignorance will consist in its subject being unable to reject certain potentially hypothetical states of the universe, each absolutely determinate in every respect, but all of which are, in fact, false. The aggregate of these unrejected falsities constitute the ‘range of possibility,’ or better, ‘of ignorance.’ Were there no ignorance, this aggregate would be reduced to zero. The state of knowledge supposed is, in necessary propositions, usually fictitious, in possible propositions more often the actual state of the speaker. The necessary proposition asserts that, in the assumed state of knowledge, there is no case in the whole range of ignorance in which the proposition is false. In this sense it may be said that an impossibility underlies every necessity. The possible proposition asserts that there is a case in which it is true.
Various subtleties are encountered in the study of modality. Thus, when the thinker's own state of knowledge is the one whose range of ignorance is in question, the judgments ‘A is true’ and ‘A must be true’ are not logically equivalent, the latter asserting a fact which the former does not assert, although the fact of its assertion affords direct and conclusive evidence of its truth. The two are analogous to ‘A is true’ and ‘A is true, and I say so’; which are readily shown not to be logically equivalent by denying each, when we get ‘A is false’ and ‘If A is true, I do not say so.’
In the necessary particular proposition and the possible universal proposition there is sometimes a distinction between the ‘composite’ and ‘divided’ senses. ‘Some S must be P,’ taken in the composite sense, means that there is no case, in the whole range of ignorance, where some S or other is not P; but taken in the divided sense, it means that there is some S which same S remains P throughout the whole range of ignorance. So ‘Whatever S there may be may be P,’ taken in the composite sense, means that there is, in the range of ignorance, some hypothetic state of things (or it may be the unidentifiable true state, though this can hardly be the only such case) in which there either is no S, or every S there is is P; while in the divided sense, it means that there is no S at all in any hypothetic state but what is some hypothetic state or other is P. When there is any such distinction, the divided sense asserts more than the composite in necessary particular propositions, and less in possible universal. But in most cases the individuals do not remain identifiable throughout the range of possibility, when the distinction falls to the ground. It never applies to necessary universal propositions or to possible particular propositions.
Some logicians say that ‘S may be P’ is not a proposition at all, for it asserts nothing. But if it asserted nothing, no state of facts could falsify it, and consequently the denial of it would be absurd. Now let S be ‘some self-contradictory proposition,’ and let P be ‘true.’ Then the possible proposition is ‘Some self-contradictory proposition may be true,’ and its denial is ‘No self-contradictory proposition can be true,’ which can hardly be pronounced absurd. It is true that those logicians usually take the form ‘S may be P’ in the copulative sense ‘S may be P, and S may not be P,’ but this only makes it assert more, not less. The possible proposition, then, is a proposition. It not only must be admitted among logical forms, if they are to be adequate to represent all the facts of logic, but it plays a particularly important part in the theory of science. See SCIENTIFIC METHOD. At the same time, according to the view of modality now under consideration, necessary and possible propositions are equipollent with certain assertory propositions; so that they do not differ from assertory propositions as universal and particular propositions differ from one another, but rather somewhat as hypothetical (i.e. conditional, copulative, and disjunctive), categorical, and relative propositions differ from one another—perhaps not quite so much.
According to this view, logically necessary and possible propositions relate to what might be known, without any knowledge whatever of the universe of discourse, but only with a perfectly distinct understanding of the meanings of words; geometrically necessary and possible propositions, to what a knowledge of the properties of space does or does not exclude; physical necessity, to what a knowledge of certain principles of physics does or does not exclude, &c. But when we say that of two collections one must be correspondentially greater than the other, but each cannot be correspondentially greater than the other, it has not been shown how this kind of necessity can be explained on the above principles.
The earliest theory of modality is Aristotle's, whose philosophy, indeed, consists mainly in a theory of modality. The student of Aristotle usually begins with the Categories; and the first thing that strikes him is the author's unconsciousness of any distinction between grammar and metaphysics, between modes of signifying and modes of being. When he comes to the metaphysical books, he finds that this is not so much an oversight as an assumed axiom; and that the whole philosophy regards the existing universe as a performance which has taken its rise from an antecedent ability. It is only in special cases that Aristotle distinguishes between a possibility and an ability, between a necessity and a constraint. In this, he is perhaps nearer the truth than the system of equipollencies set forth above.
Kant seems to have been the first to throw any light upon the subject. To the old distinction between logical and real possibility and necessity, he applied two new pairs of terms, analytic and synthetic, and subjective and objective. The following definitions (where every word is studied) certainly advanced the subject greatly:—
‘1. Was mit den formalen Bedingungen der Erfahrung (der Anschauung und den Begriffen nach) übereinkommt, ist möglich.
‘2. Was mit den materialen Bedingungen der Erfahrung (der Empfindung) zusammenhängt, ist wirklich.
‘3. Dessen Zusammenhang mit dem Wirklichen nach allgemeinen Bedingungen der Erfahrung bestimmt ist, ist (existirt) nothwendig’ (Krit. d. reinen Vernunft, 1st ed., 219).
Kant holds that all the general metaphysical conceptions applicable to experience are capable of being represented as in a diagram, by means of the image of time. Such diagrams he calls ‘schemata.’ The schema of the possible he makes to be the figure of anything at any instant. The schema of necessity is the figure of anything lasting through all time (ibid., 144, 145). He further states (ibid., 74, footnote; Jäsche's Logik, Einl. ix, and elsewhere) that the possible proposition is merely conceived but not judged, and is a work of the apprehension (Verstand); that the assertory proposition is judged, and is, so far, a work of the judgment; and that the necessary proposition is represented as determined by law, and is thus the work of the reason (Vernunft). He maintains that his deduction of the categories shows that, and how, the conceptions originally applicable to propositions can be extended to modes of being—constitutively, to being having reference to possible experience; regulatively, to being beyond the possibility of experience.
Hegel considers the syllogism to be the fundamental form of real being. He does not, however, undertake to work over, in the light of this idea, in any fundamental way, what is ordinarily called logic, but which, from his point of view, becomes merely subjective logic. He simply accepts Kant's table of functions of judgment, which is one of the most ill-considered performances in the whole history of philosophy. Consequently, what Hegel says upon this subject must not be considered as necessarily representing the legitimate outcome of his general position. His followers have been incompetent to do more. Rosenkranz (Wissenschaft d. logischen Idee) makes modality to represent the superseding of the form of the judgment and to be the preparation for that of the syllogism. In the Encyclopädie, Hegel's last statement, §§ 178-80, we are given to understand that the judgment of the Begriff has for its contents the totality (or, say, conformity to an ideal). In the first instance, the subject is singular, and the predicate is the reflection of the particular object upon the universal. That is, this or that object forced upon us by experience is judged to conform to something in the realm of ideas. But when this is doubted, since the subject does not, in itself, involve any such reference to the ideal world, we have the ‘possible’ judgment, or judgment of doubt. But when the subject is referred to its genus, we get the apodictic judgment. But Hegel had already developed the ideas of possibility and necessity in the objective logic as categories of Wesen. In the Encyclopädie the development is somewhat as follows: Wirklichkeit is that whose mode of being consists in self-manifestation. As identity in general (the identity of Sein and Existenz) it is, in the first instance, possibility. That is to say, apparently, bare possibility, any fancy projected and regarded in the aspect of a fact. It is possible, for example, that the present Sultan may become the next Pope. But in the second movement arise the conceptions of the Zufällig, Aeusserlichkeit, and ‘condition.’ The Zufällig is that which is recognized as merely possible: ‘A may be, but A may not be’; but it is also described by Hegel as that which has the Grund, or antecedent of its being, in something other than itself. The Aeusserlichkeit seems to be the having a being outside the ground of its being—an idea assimilated to caprice. That which such Aeusserlichkeit supposes outside of itself, as the antecedent of its being, is the presupposed condition. The third movement gives, in the first instance, ‘real possibility.’ In this we find the conceptions of ‘fact’ (Sache), ‘activity’ (Thätigkeit), and ‘necessity.’
Lotze and Trendelenburg represent the first struggles of German thought to rise from Hegelianism. The most remarkable characteristic of Lotze's thought is, that he not only sees no urgency for unity of conception in philosophy, but holds that such unity would inevitably involve a falsity. He represents a judgment as a means of apprehending becoming, in opposition to the concept, which apprehends being; but he says that the business of the judgment is to supply the cement for building up concepts. Accordingly, he has no doctrine of modality as a whole, but merely considers three cases, between which he traces no relation. Necessity may arise either out of the universal analytic judgment, the conditional judgment, or the disjunctive judgment. By the ‘judgment’ is meant the meaning of a proposition. Lotze finds that the meaning of the analytical judgment is illogical, since it identifies contraries. However, the meaning of this meaning is justified by its not meaning to mean that the terms are identical, but only that the objects denoted by those terms are identical. The analytic proposition is, therefore, admissible, because it is practically meant to mean a particular proposition, that is, one in which the predicate is asserted of all the particulars. And the justification of the proposition, whose use was to be to connect elements of terms, is that, meant not as it is meant, but as it is meant to be meant, these elements are identical and do not need to be connected. In this way Lotze vindicates the necessity of the analytical categorical proposition. Coming next to conditionals, by thought of the same order, he finds that, assuming that the universe of real, intelligible objects is ‘coherent,’ we may be justified in asserting that the introduction of a condition X into a subject S gives rise to a predicate P as an analytical necessity; and for this purpose, when it is once accomplished, it does not matter whether the ladder of the assumption of coherence remains or is taken away. Lotze treats the disjunctive proposition last, as if it were of a higher order, following Hegel in this respect. But what was excusable for Hegel is less so for Lotze, since he himself had signalized the significance of impersonal propositions, such as ‘it rains,’ ‘it thunders,’ ‘it lightens,’ whose only subject is the universe. Now, if there is any difference between ‘If it lightens, it thunders,’ and ‘Either it does not lighten or it thunders,’ it is that the latter considers the actual state of things alone, and the former a whole range of other possibilities. However, Lotze considers last the propositional form ‘S is P1 or P2 or P3.’ Properly, this is not a disjunctive proposition, but only a proposition with a disjunctive predicate. Lotze considers it a peculiar form, because it cannot be represented by an Euler's diagram, which is simply a blunder. The necessity to which it gives rise must, therefore, either be the same as the conditional necessity, or else differ from it merely by greater simplicity. For other sound objections to Lotze's theory see Lange, Logische Studien, ii.
Trendelenburg (Logische Untersuch., xiii) maintains that possibility and necessity can only be defined in terms of the antecedent (Grund), though we might, perhaps, object to the translation of Grund by so purely formal a word as ‘antecedent,’ notwithstanding its harmony with Aristotle. If all conditions are recognized, and the fact is understood from its entire Grund, so that thought quite permeates being—a sort of phrase which Trendelenburg always seeks—there is ‘necessity.’ If, on the other hand, only some conditions are recognized, but what is wanting in Grund is made up in thought, there is ‘possibility.’ In itself, an egg is nothing but an egg, but for thought it may become a bird. Trendelenburg will, therefore, neither admit, with Kant, that modality is originally a mere question of the attitude of the mind, nor with Hegel, whom he criticizes acutely, that it is originally objective.
Sigwart, who holds that logical questions must ultimately be decided by immediate feeling, and that the usages of the German language are the best evidence of what that feeling is, denies that the possible proposition is a proposition at all, because it asserts nothing. He forgets that if a proposition asserts nothing, the denial of it must be absurd, since it must exclude every possibility. Now, the denial of ‘I do not know but that A may be true’ is ‘I know A is not true,’ which is hardly absurd. Sigwart, it is true, in accordance with usages of speech, takes ‘A may be true’ in what the old logicians called the sensus usualis, that is, for the copulative proposition ‘A may be true, and further A may be not true.’ But this does not make it assert less, but more, than the technical form. In regard to the necessary proposition, Sigwart, following his guide, the usages of speech, finds that ‘A must be true,’ asserts less than ‘A is true,’ so that from the latter the former follows, but not at all the latter from the former. This may be true for the usages of German speech, just as such phrases as ‘beyond every shadow of doubt,’ ‘out of all question,’ and the like, in our vernacular commonly betray the fact that there is somebody who not only doubts and questions, but flatly denies, the proposition to which they are attached. Bradley accepts the sensational discovery of Sigwart.
Lange (loc. cit.) thinks the matter is put in the clearest light by the logical diagrams usually attributed to Euler, but really going back to Vives. ‘We, therefore, here again see,’ he says, ‘how spatial intuition, just as in geometry, verifies (begründet) a priority and necessity.’ (C.S.P.)
Modulus [Lat. modus, a mode]. (1) Proposed by Schröder (Ger. Modul; Fr. not in use; Ital. modulo, suggested—E.M.) for the four relative terms upon which the logic of dual RELATIVES (q.v.) hinges; namely, ‘Not,’ ‘Same as,’ Excluded from a universe containing,’ and ‘With, or within a universe containing.’
These terms were first called by Peirce the ‘definite dual relatives of second intention’; he now thinks it might be well to term these the four ‘cardinals,’ or four cardinal dual relatives.
Literature: PEIRCE, in Studies in Logic by Members of the Johns Hopkins University, 191, and Amer. J. Math., iii. 47; SCHRÖDER, Algebra d. Logik, iii. 117.
(2) See ERRORS OF OBSERVATION. (C.S.P.)
Modus ponens and Modus tollens [Lat.]. Two ways of reasoning from a conditional proposition or consequence. The modus ponens from the consequence and the antecedent infers the consequent; the modus tollens from the consequence and the falsity of the consequent infers the falsity of the antecedent, thus:
Modus Ponens. If A is true, C is true; A is true; \ C is true.
Modus Tollens. If A is true, C is true; C is false; \ A is false.
A third way of reasoning, namely, from the truth of the antecedent and falsity of the consequent to the falsity of the consequence, is generally overlooked. See HYPOTHETICAL (syllogism). (C.S.P.)
Monad (Monadism, Monadology) [Gr. μονας, unit]: Ger. Monade; Fr. monade; Ital. monade. In ancient philosophy, the unit in arithmetic, or unity as opposed to duality; it figures in this sense in the numerical speculations of the Platonic school and the later Pythagoreans. The special case of the number two, considered as unit or constituent of being, was known to the Pythagoreans as the Dyad (for Zenocrates' doctrine of the Dyad see ONE). (A.S.P.P.- J.M.B.)
(1) With the Pythagoreans, the monad was the number one considered, as well as we can make out, as the first creative deity (Zeller).
(2) In other Greek schools a monad is simply an individual. With the Atomists, an atom.
(3) In the philosophy of Leibnitz a monad is a being pursuing its development according to an inward law, in pre-established harmony with other beings. The idea may be illustrated by two pendulums, each moving according to a formula of its own. This illustration is used by Leibnitz himself. This theory has been resuscitated by Renouvier (La Nouvelle Monadologie, Paris, 1898).
(4) In the logic of RELATIVES (q.v.), a proposition with one term left blank, to be filled in if the proposition is to be completed. In chemistry: a radicle with one free bond. (C.S.P.)
Multitude (in mathematics) [Lat. multitudo]: Ger. Mächtigkeit, Cardinalzahl; Fr. puissance; Ital. moltitudine. That relative character of a collection which makes it greater than some collections and less than others. A collection, say that of the A's, is greater than another, say that of the B's, if, and only if, it is impossible that there should be any relation r, such that every A stands in the relation r to a B to which no other A is in the relation r.
The precise analysis of the notion is due to G. Cantor, whose definition is, however, a little different in its mode of expression, since it is more abstract. He defines the character in these words: ‘By Mächtigkeit or cardinal number of a collection (Menge) M, we mean the universal concept, which by the help of our active faculty of thought results from the collection M by abstraction from the characters of the different members (Elemente) of that collection and from the order in which they are given (Gegebensein).’
A cardinal number, though confounded with multitude by Cantor, is in fact one of a series of vocables the prime purpose of which, quite unlike any other words, is to serve as an instrument in the performance of the experiment of counting; these numbers being pronounced in their order from the beginning, one as each member of the collection is disposed of in the operation of counting. If the operation comes to an end by the exhaustion of the collection, the last cardinal number pronounced is applied adjectivally to the collection, and expresses its multitude, by virtue of the theorem that a collection the counting of which comes to an end, always comes to an end with the pronunciation of the same cardinal number.
If the cardinal numbers are considered abstractedly from their use in counting, simply in themselves, as objects of mathematical reasoning, stripped of all accidents not pertinent to such study, they become indistinguishable from the similarly treated ordinal numbers, and are then usually called ordinal numbers by the mathematico-logicians. There is small objection to this; yet it is to be remarked that they are ordinal in different senses in grammar and in the logic of mathematics. For in grammar they are called ordinal as being adapted to express the ordinal places of other things in the series to which those things belong; while in the logic of mathematics the only relevant sense in which they are ordinal is as being defined by a serial order within their own system. The definition of this order is not difficult; but the syntax of ordinary language does not lend itself to the clear expression of such relations in the manner in which they ought to be expressed in order to bring out their logical character. It must, therefore, be here passed by. In fact, none of the doctrines of logic can be satisfactorily expressed under the limitations here imposed, however simple they may be. The doctrine of ordinal numbers is by Dedekind (Was sind und was sollen die Zahlen?) made to precede that of the cardinal numbers; and this is logically preferable, if hardly so imperative as Schröder considers it.
The doctrine of the so-called ordinal numbers is a doctrine of pure mathematics; the doctrine of cardinal numbers, or, rather, of multitude, is a doctrine of mathematics applied to logic. The smallest multitude is most conveniently considered to be zero; but this is a question of definition. A finite collection is one of which the syllogism of transposed quantity holds good. Of finite collections, it is true that the whole is greater than any part. It is singular that this is often taken as the type of an axiom, although it has from early times been a matter of familiar knowledge that it is not true of infinite collections. Every addition of one increases a finite multitude. An infinite collection cannot be separated into a lesser collection of parts all smaller than itself.
The multitude of all the different finite multitudes is the smallest infinite multitude. It is called the denumeral multitude. (Cantor uses a word equivalent to denumerable; but the other form has the advantage of being differentiated from words like enumerable, abnumerable, which denote classes of multitudes, not, like denumeral, a single multitude.) Following upon this is a denumeral series of multitudes called by C. S. Peirce the first, second, &c. abnumerable multitudes. Each is the multitude of possible collections formed from the members of a collection of the next preceding multitude. They seem to be the same multitudes that are denoted by Cantor as Alephs. The first of them is the multitude of different limits of possible convergent series of rational fractions, and therefore of all the quantities with which mathematical analysis can deal under the limitations of the doctrine of limits. (The imaginaries do not increase the multitude.) What comes after these is still a matter of dispute, and is perhaps of inferior interest. The transition to continuity is, however, a matter of supreme importance for the theory of scientific method; nor is it a very complicated matter; but it cannot be stated under the limitations of expression here imposed upon us. (C.S.P., H.B.F.)
Literature: see NUMBER.
Name (in logic). Two quite different sorts of terms are called in logic names. A proper name serves to call to mind an individual object of experience well known both to the speaker and hearer (for if the object is not known to the hearer it is only just beginning to fulfil for him the function of a proper name), and to show that it is that object concerning which information is furnished or desired. Many proper names are names of collective individuals; and a few are grammatically plural, as the Gracchi. A common name, usually now called a class-name in logic, though common name is better, has a signification as well as a denotation. That is to say, it conveys the idea that whatever it may be that is spoken of it is of a certain indicated general description, which may be in some sense negative.
Abstract names are common names of fictitious objects which correspond to predicates. At first sight they appear to be mere convenient superfluities; for to say that opium has a soporific virtue, is precisely the same thing as to say that opium puts people to sleep. But closer examination shows that abstract words enable us to express relations which could not otherwise be expressed. A relation is something true of a set of objects. But abstractions enable us to express a fact true of a set of sets of objects. Every collective name is an abstract name; and it would be a want of discrimination to say that numbers are superfluities. Moreover, when we see what the true nature of abstract names is, we must confess that their objects may be just as real as the objects of concrete names. They are fictitious only in the sense of having been made up out of concrete names. An abstract name may be regarded as the name of a fictitious individual; and when this individual is perfectly indescribable, like the quality of a simple sensation, the abstract name may perhaps be more like a proper name than like a common name.
Names are divided into names of first imposition and names of second imposition, which latter are names applicable to words, as pronoun, conjunction, &c. The precise definition is given by Ockham, Logica, Pars I, cap. xi. Names are also divided into names of first and of second intention. See TERM. (C.S.P.)
Necessary (in logic): Ger. nothwendig; Fr. nécessaire; Ital. necessario. That is necessary which not only is true, but would be true under all circumstances.
Something more than brute compulsion is, therefore, involved in the conception; there is a general law under which the thing takes place. Thus necessity, in the philosophical sense, is quite opposed to any ‘Noth’ that ‘kennt kein Gebot.’ Springing from law, and thus being essentially rational, it would perhaps be more accurately described as persuasive than as compulsive.
The Stoics defined the necessary as ‘that which, being true, is not susceptible of becoming false, or, if it be so, is prevented from ever becoming false’ (Diog. Laer., vii. 75). Kant defines the necessary as that which is a priori certain (Krit. d. reinen Vernunft, 1st ed., 125).
Necessary adjunct: a phrase which a very improper usage makes to signify a property, that is, an inessential predicate, not only belonging at all times to every individual of the species of which it is a necessary adjunct, but further, belonging to nothing else.
Necessary cause: one which acts by a necessity of its nature and is not free.
Necessary object, says Kant, is one which is determined according to concepts by the connection of perceptions (Krit. d. reinen Vernunft, 1st ed., 234).
Necessary sign: a sure indication. (C.S.P.)
Necessity [Lat. necessitas]: Ger. Nothwendigkeit; Fr. nécessité; Ital. necessità. [The main part of this entry is by (J.D.); only the final part, given here, is by Peirce.]
The following distinctions are usual:
Internal necessity springs from the nature of the subject of the necessity; external necessity comes from the outside.
Internal necessity is either absolute or secundum quid. Absolute necessity belongs to that whose being otherwise would involve contradiction. Necessity secundum quid is that which depends upon some matter of fact. Thus the Aristotelians held that a body falls to the ground by a necessity of its own nature, without external force or agency; yet it is easily prevented from falling.
External necessity, also called necessity ex hypothesi, because depending on an external condition, is distinguished in whatever ways the necessary is distinguished in the doctrine of the MODAL (q.v.), and, in particular, in reference to the sensus compositus and sensus divisus. In addition, external necessity is divided according as the realization of the condition precedes, is contemporaneous with, or follows after, the necessary result. Necessity from a previous condition is either that due to God's fore-knowledge or it is causal. Causal necessity (used also in modern logic) is either necessity of compulsion or necessity of determination.
Necessity determined by a subsequent condition is either ex hypothesi finis or ex hypothesi eventus (as the apostle says, ‘it is necessary that offences should come’). Necessity ex hypothesi finis is either ad esse or ad bene esse.
Another common distinction is between necessity in causando, in essendo, and in praedicando, phrases which explain themselves.
Still another threefold distinction, due to Aristotle (I Anal. post., iv), is between necessity de omni (το κατα παντος), per se (καθ’ αὐτο), and universaliter primum (καθολου πρωτον). The last of these, however, is unintelligible, and we may pass it by, merely remarking that the exaggerated application of the term has given us a phrase we hear daily in the streets, ‘articles of prime necessity.’ Necessity de omni is that of a predicate which belongs to its whole subject at all times. Necessity per se is one belonging to the essence of the species, and is subdivided according to the senses of per se, especially into the first and second modes of per se.
Among modern distinctions we may mention that of Benno Erdmann between predicative and deductive necessity. The former seems to be necessity for a judgment being as it is in order to express what is in its immediate object.
Logical necessity is determined by the laws of the understanding, according to Kant (Krit. d. reinen Vernunft, 1. Aufl., 76).
Metaphysical necessity is that of God's existence.
Simple = absolute necessity. See above.
The adjectives by which different kinds of necessity are usually distinguished include absolute, antecedent, causal, comitant, composite, consequent, deductive, disjunct, disjunctive, external, formal, hypothetical, immediate, internal, logical, material, mediate, metaphysical, modal, moral, physical, practical, predicative, prime, simple, teleological, unconditional. (C.S.P.)
Negation [Lat. negatio, which translates Gr. ἀποφασις]: Ger. Verneinung; Fr. négation; Ital. negazione. Negation is used (1) logically, (2) metaphysically. In the logical sense it may be used (a) relatively, and (b) absolutely. Used relatively, when applied to a proposition, it may be understood (α) as denying the proposition, or (β) as denying the predicate.
(1) In its logical sense, negation is opposed to affirmation, although, when it is used relatively, this is perhaps not a convenient contrary term; in its metaphysical sense, negative is opposed to positive (fact, &c.).
The conception of negation, objectively considered, is one of the most important of logical relations; but subjectively considered, it is not a term of logic at all, but is pre-logical. That is to say, it is one of those ideas which must have been fully developed and mastered before the idea of investigating the legitimacy of reasonings could have been carried to any extent.
The treatment of the doctrine of negation affords a good illustration of the effects of applying the principle of PRAGMATISM (q.v.) in logic. The pragmatist has in view a definite purpose in investigating logical questions. He wishes to ascertain the general conditions of truth. Now, without of course undertaking to present here the whole development of thought, let it be said that it is found that the first step must be to define how two propositions can be so related that under all circumstances whatsoever,
This must be the first part of logic. It is deductive logic, or (to name it by its principal result) syllogistic. At all times this part of logic has been recognized as a necessary preliminary to further investigation. Deductive and inductive or methodological logic have always been distinguished; and the former has generally been called by that name.The truth of the one entails the truth of the other,
The truth of the one entails the falsity of the other,
The falsity of the one entails the truth of the other,
The falsity of the one entails the falsity of the other.
In order to trace these relations between propositions, it is necessary to dissect the propositions to a certain extent. There are different ways in which propositions can be dissected. Some of them conduce in no measure to the solution of the present problem, and will be eschewed by the pragmatist at this stage of the investigation. Such, for example, is that which makes the copula a distinct part of the proposition. It may be that there are different ways of useful dissection; but the common one, which alone has been sufficiently studied, may be described as follows:
Taking any proposition whatever, as
‘Every priest marries some woman to some man,’we notice that certain parts may be struck out so as to leave a blank form, in which, if the blanks are filled by proper names (of individual objects known to exist), there will be a complete proposition (however silly and false). Such blank forms are, for example:
Every priest marries some woman to ______,
_____ marries _____ to some man,
_____ marries _____ to _____.
It may be that there is some language in which the blanks in such forms cannot be filled with proper names so as to make perfect propositions, because the syntax may be different for sentences involving proper names. But it does not matter what the rules of grammar may be.
The last of the above blank forms is distinguished by containing no selective word such as some, every, any, or any expression equivalent in force to such a word. It may be called a PREDICATE (q.v., sense 2) or ῥημα. Corresponding to every such predicate there is another, such that if all the blanks in the two be filled with the same set of proper names (of individuals known to exist), one of the two resulting propositions will be true, while the other is false; as
Chrysostom marries Helena to Constantine;It is true that the latter is not good grammar; but that is not of the smallest consequence. Two such propositions are said to be contradictories, and two such predicates to be negatives of one another, or each to result from the negation of the other. Two propositions involving selective expressions may be contradictories; but in order to be so, each selective has to be changed from indicating a suitable selection to indicating any selection that may be made, or vice versa. Thus the two following propositions are contradictories:
Chrysostom non-marries Helena to Constantine.
Every priest marries some woman to every man;It is very convenient to express the negative of a predicate by simply attaching a non to it. If we adopt that plan, non-non-marries must be considered as equivalent to marries. It so happens that both in Latin and in English this convention agrees with the usage of the language. There is probably but a small minority of languages of the globe in which this very artificial rule prevails. Of two contradictory propositions each is said to result from the negation of the other.
Some priest non-marries every woman to some man.
The relation of negation may be regarded as defined by the principles of contradiction and excluded middle. See LAWS OF THOUGHT. That is an admissible, but not a necessary, point of view. Out of the conceptions of non-relative deductive logic, such as consequence, coexistence or composition, aggregation, incompossibility, negation, &c., it is only necessary to select two, and almost any two at that, to have the material needed for defining the others. What ones are to be selected is a question the decision of which transcends the function of this branch of logic. Hence the indisputable merit of Mrs. Franklin's eight copula-signs, which are exhibited as of co-ordinate formal rank. But, so regarded, they are not properly copulas or assertions of the relation between the several individual subjects and the predicate, but mere signs of the logical relations between different components of the predicate. The logical doctrine connected with those signs is of considerable importance to the theory of pragmatism.
For the negation of modals see MODAL.
Conversion by negation = CONTRAPOSITION (q.v.).
Negant or negative negation is the negation effected by attaching the negative particle to the copula in the usual Latin idiom, ‘Socrates non est stultus,’ in contradistinction to infinite (ἀοριστη), or infinitant, negation, which is effected by attaching the negative particle to the predicate, ‘Socrates est non stultus.’
Kant revived this distinction in order to get a triad to make out the symmetry of his table of categories; and it has ever since been one of the deepest and dearest studies of German logicians. No idea is more essentially dualistic, and distinctly not triadic, than negation. Not-A = other than A = a second thing to A. Language preserves many traces of this. Dubius is between two alternatives, yea and nay.
(2) In the metaphysical sense, negation is the mere absence of a character or relation that is regarded as positive. It is distinguished from privation in not implying anything further.
Spinoza's celebrated saying, of which the Schellings have made so much, ‘omnis determinatio est negatio,’ has at least this foundation, that determinatio to one alternative excludes us from another. The same great truth is impressed upon youth in the utterance: ‘You cannot eat your cake and have it too’. (C.S.P., C.L.F.; the final paragraph of this entry, p. 147-8, by C.L.F. and J.M.B., is not given here.)
Negative [Lat. negativa; a term appearing first in logic in Boethius, in place of the previous abdicativa, although negatio was much earlier. It translates Aristotle's ἀποφατικη. Cognate words were used by Plato, and even earlier]: Ger. verneinend; Fr. négatif; Ital. negativo. Involving NEGATION (q.v.), either in the second application of the logical sense, or in the metaphysical sense given under that term.
Negative abstraction is an act of abstraction derived from considering something which does not possess the character considered.
Negative (or necessary) condition: see NECESSARY AND SUFFICIENT CONDITION.
Negative criterion: a criterion which is a negative condition; a test. Most criteria are of this sort.
Negative discrepancy: see DISCREPANCY.
Negative distinction: a mutual real distinction separating anything from its negation; as the distinctions of heat and cold (no heat), light and darkness (no light), sound and silence (no sound).
Negative idea: see Negative name.
Negative mark: a mark which consists in the non-occurrence of a positive phenomenon under certain conditions.
Negative name: a common name which characterizes an object by its want of some character. ‘I appeal,’ says Locke, ‘to every one's own experience, whether the shadow of a man, though it consists of nothing but the absence of light (and the more the absence of light is, the more discernible is the shadow), does not, when a man looks on it, cause as clear and positive an idea in his mind as a man himself, though covered over with clear sunshine? And the picture of a shadow is a positive thing. Indeed, we have negative names, which stand not directly for positive ideas, but for their absence, such as insipid, silence, nihil, &c., which words denote the positive ideas, taste, sound, being, with a signification of their absence’ (Essay concerning Human Understanding, II. viii. 5).
Negative negation: see NEGATION.
Negative syllogism: any syllogism of the second figure, or the modus tollens, where the reasoning turns upon the change of quality. The canon of syllogism, that nothing can be concluded from two negatives, is inaccurate. What is requisite, in non-relative syllogism, is that the middle term should be once distributed and once undistributed. Darapti and Felapton, which appear to violate this rule, only do so because one of the premises, so far as it is efficient, is virtually a particular. What is requisite is, that one of the interlocutors should select the individual denoted by the middle term in one premise and the other in the other.
Negative whole is one which has no parts; as God, the soul, &c. (C.S.P.; followed by C.L.F.'s definition of Negative Term, p. 148-9, not given here.)
Nominal [Lat. nominalis, pertaining to a name]: Ger. nominal; Fr. nominal; Ital. nominale. Relating to a logical term, whether expressed in language or merely a concept of the mind, and not to anything real. Cf. NOMINALISM, and REALISM.
Nominal definition (definitio nominis): the declaration of the essence of a word or expression, that is, the necessary and sufficient conditions of its applicability, or the enumeration of marks which suffice, but do not more than suffice, to give the meaning of the term, understanding by the ‘meaning,’ not the whole idea it may convey, but so much as it would require to be intended to convey in order to be a suitable word. Leibnitz says, ‘Habemus quoque discrimen inter definitiones nominales, quae notas tantum rei ab aliis discernendae continent, et reales, ex quibus constat rem esse possibilem, et hac ratione satisfit Hobbio, qui veritates volebat esse arbitrarias, quia ex definitionibus nominalibus penderent, non considerans realitatem definitionis in arbitrio non esse, nec quaslibet notiones inter se posse coninungi. Nec definitiones nominales sufficiunt ad perfectam scientiam, nisi quando aliunde constat rem definitam esse possibilem.’ This mode of making the distinction has been approved by many nominalists, as J. S. Mill. It cannot satisfy the realists, who demand of the real definition that it should express the real generating nature of the real species which it defines. As for the possibility of the thing, if by that is meant logical possibility, the nominal definition suffices. If more than that is meant, it is out of the province of definition to prove or declare a thing to be possible; a ‘problem’ proves such possibility.
Nominal mode, in the doctrine of modals: a mode of a proposition expressed by an adjective, as ‘Sortem currere est contingens.’ (C.S.P.)
Nomology [Gr. νομος, law, + λογος, doctrine]: for equivalents see the next topic. The science which investigates laws, as general psychology and general physics; contradistinguished from classificatory and explanatory science. Hamilton says, ‘We have a science which we may call the nomology of mind—nomological psychology’ (Lects. on Met., vii). (C.S.P.)
Non-A (in logic): same in the other languages. An expression occurring in the usual forms of statement of the principles of contradiction and excluded middle. It is a term which denotes whatever is supposed not to be denoted by A, and denotes nothing more. (C.S.P.)
Non-contradiction. The ‘law of non-contradiction’ is another name for the principle of CONTRADICTION (q.v.). See also LAWS OF THOUGHT. (C.S.P.)
Non sequitur [Lat. for ‘it does not follow’]. A name which belongs to the slang of the universities for the fallacia consequentis (called by Aristotle ὁ παρα το ἑπομενον ἐλεγχος, De Sophist. Elen., 167 b 1), which is, strictly speaking, a fallacy which arises from a simple conversion of a universal affirmative, or transposing a protasis and apodsis, or condition and consequent.
Thus Aristotle tells us that the Eleatic Melissus argued that the universe is ungenerated, since nothing can be generated by what does not previously exist. The universe, then, not being generated, had no beginning; and having no beginning, it is infinite. But, as Aristotle remarks, although everything generated has a beginning, it does not follow (non sequitur, οὐκ ἀναγκη δε τουτο συμβαινειν) that everything that has a beginning is generated. A fever, for example, is not generated. Such fallacies are extremely common. De Morgan (Formal Logic, 268) gives this example: ‘Knowledge gives power, power is desirable, therefore knowledge is desirable.’ But though whatever is desirable has some desirable effect, it does not follow that whatever has any desirable effect is desirable. An attack of yellow fever has the desirable effect of rendering it unlikely the patient will for a long time have another; still, it is not itself desirable.
But the majority of logicians not only confound this fallacy with the post hoc, ergo propter hoc, which Aristotle considers immediately after, but even define it as ‘failure in the formal inadequacy of the reason’ (Sidgwick, Fallacies, II. ii. 4), or as ‘the introduction of new matter into the conclusion, which is not contained in the premises’ (Hyslop, Logic, xviii. 2), or as ‘the simple affirmation of a conclusion which does not follow from the premises’ (De Morgan, loc. cit.), or as ‘any argument which is of so loose and inconsequent a character that no one can discover any cogency in it’ (Jevons, Lessons in Logic, xxi), or ‘to assume without warrant that a certain conclusion follows from premises which have been stated’ (Creighton, Introductory Logic, § 46). Very many logicians omit it altogether, which is better.
Aristotle, however, could not express himself more precisely: Ὁ παρα το ἑπομενον ἐλεγχος δια το οἰεσθαι ἀντιστρεφειν την ἀκολουθησιν. That is, ‘from thinking that the consequentia can be converted.’ That is to say, thinking that because ‘If A, then C,’ therefore ‘If C, then A.’ Owing to the neglect of fallacies by the more scientific logicians, it is not easy to cite many who define the fallacy correctly. The Conimbricenses (than whom no authority is higher) do so (Commentarii in Univ. Dialecticam Arist. Stagir., In lib. Elench., q. i. art. 4); also Eustachius (Summa Philos., Tom. I, pars. III, tract. iii, disput. iii. 9. 3); also Cope, an admirable student of Aristotle, in his note on the Rhetorics, B. cap. xxiv. See also the Cent. Dict., under ‘Fallacy.’ (C.S.P.)
Norm (and Normality) [Lat. norma, a carpenter's square, a rule]: Ger. Norm, Normalität; Fr. norme, normalité; Ital. norma, normalità. (1) A standard type or pattern from which continuous departures are possible in opposite directions. (C.S.P.; def. (2) by J.J. omitted here.)
Nota notae [Lat.]: The logical principle Nota notae est nota rei ipsius, that is, the predicate of the predicate is the predicate of the subject, which is laid down in several places by Aristotle as the general principle of syllogism. The principle passages are as follows:—
‘When one thing is predicated of another as its subject, whatever is said of the predicate can also be said of the subject’ (Categ., iii. 1 b 10).
‘Whatever is said of the predicate will hold also of the subject’ (Categ., v. 3 b 4).
‘We say that something is predicated universally when nothing can be admitted as coming under the subject of which the predicate will not hold; and the same thing holds of negation’ (1 Anal. pr., i. 24 b 28). The term nota notae is from the first words of the original of this passage.
‘Of whatever the species is predicated, the genus is predicable’ (Topics, Δ. i. 121 a 25).
Some writers (as Hamilton, Lects. on Logic, App. VI. ii) imagine a distinction between the nota notae and the dictum de omni. Some have been so extravagant as to attribute the former to Kant, in whose Falsche Spitzfindigkeit (1762, ii) it is very likely that the precise phrase ‘nota notae est nota rei ipsius’ first occurs, though similar phrases, such as ‘cui convenient notae eidem quoque convenit nomen,’ are common in Wolf's and other logics of the 18th century. But it is clear that in Aristotle's mind it was one principle, essentially that which De Morgan well called the principle of the ‘transitiveness of the copula.’
Aristotle, in the last but one of the above passages, seems to regard the nota notae as following from the definition of universal predication. To say that ‘Any S is P’ is to say that of whatever S is true, P is true. This amounts to deriving the transitiveness of the copula from the transitiveness of illation. If from A follows B and from B follows C, then from A follows C. This, again, is equivalent to the principle that to say that from the truth of X follows the truth of the consequence that from Y follows Z, is the same as to say that from the joint truth of X and Y follows Z. (C.S.P.)
Numerical [Lat. numerus, number]: Ger. Zahl- (in compounds, as Zahldifferenz); Fr. numérique; Ital. numerico, numerale. If two bodies move in the same orbit and differ in no respect but that of being at any one instant in different places, they are said to be numerically different. Whether or not it is quite accurate to say that they differ only in this, that there are two of them, it is sufficiently so to account for the origin of the phrase. Numerical difference is individual difference, apart from all qualitative unlikeness. Numerical identity is being strictly the same individual. Cf. the different topics IDENTITY, DIFFERENCE, and INDIVIDUAL.
This adjective in logical phrases usually translates the Greek ἀριθμω. Some writers have doubted whether the Greek word is here to be understood in an arithmetical sense, and have seemed to suspect that it was a relic of some original and different signification of the word. But this is hardly called for.
A numerically definite syllogism is one the force of which depends upon the relations of numbers; as ‘Most of the men at a certain gathering wore dress-coats, and most of them had white neckties. Hence, some of those who wore dress-coats had white neckties.’ (C.S.P.)
Observation [Lat. observatio, from observare, to look up]: Ger. Beobachtung; Fr. observation; Ital. osservazione. Attentive experience; especially, an act of voluntarily attentive experience, usually with some, often with great, effort. Cf. the following topics.
More or less fixity in the object is requisite. Indeed, experience supposes that its object reacts upon us with some strength, much or little, so that it has a certain grade of reality or independence of our cognitive exertion. All reasoning whatever has observation as its most essential part. Whatever else there is in the act of reasoning is only preparatory to observation, like the manipulation of a physical experiment.
Much stress has been laid upon the distinction between ‘sciences of observation’ and ‘sciences of experiment’; and undoubtedly there is a great contrast between the proceedings, let us say, of the anatomist and of the physiologist. Although the anatomist has to make many experiments (with stains, for example), yet the stress of his labour comes upon the act of observation; while the preparations for observation of the physiologist are far more elaborate, and the mere act of observation itself often very easy and coarse. The difference is, however, chiefly one of degree, and from a philosophical point of view is of quite secondary importance. (C.S.P., J.M.B.)
Obversion [Lat. obversio, a turning]. Hamilton (Lects. on Logic, xiv, and especially Appendix V. iii) states that CONVERSION (q.v., also for foreign equivalents) in logic is sometimes called obversion.
This is a surprising statement, which neither he nor his editors are able to support by citations. It is, therefore, not unlikely that Hamilton took it at second hand.
Bain (Logik, Pt. I. Bk. I. chap. iii. § 27) says: ‘In affirming one thing, we must be prepared to deny the opposite: “the road is level,” “it is not inclined,” are not two facts, but the same fact from its other side. This process is called obversion.’ Bain gives no reference. The regular scholastic name for the process he describes—a name given by Abelard (Dialectica, 225)—is infinitatio. This word is very common (see, for example, Albertus Magnus in II. Peri hermeneias, iii; Ockham, Logica, II. xii, xiii; and the index to Prantl, Logik, iv). But somebody may have got the notion that it was ‘barbarous,’ and have preferred to use a more classical-sounding designation. (C.S.P.)
Opposition (in logic). One of Aristotle's POSTPREDICAMENTS (q.v.). There are said, in the book of Categories (cap. x), to be four kinds of opposites. Relative opposites are relate and correlate of a disquiparent relation. Contrary opposites are the most unlike species of the same genus, as black and white, sickness and health. The third kind of opposition is between a habit and its privation, as sight and blindness. The fourth kind is between affirmation and negation. This passage has prevented the word opposite from taking any definite meaning in philosophy. (C.S.P.)
Organon [Gr.]: the same in the other languages. Since neither the Aristotelian definition of a speculative science, nor of a practical science, nor of an art, seemed to suit logic very well, the early peripatetics and commentators denied that it was either a science or an art, and called it an instrument, ὀργανον; but they did not precisely define their meaning. It was negative chiefly. The collection of Aristotle's logical treatises, when it was made, thus came to be called the Organon.
Francis Bacon, disapproving of Aristotle's methods, wished all that to be laid aside; and he consequently called his work, which was designed to be a guide for establishing a systematic inductive procedure, Novum Organum. The name was afterwards imitated by sundry authors, as Lambert in his Neues Organon, and Whewell in his Novum Organum Renovatum. (C.S.P.)
P (in logic). (1) The predicate of a judgment.
(2) The major term of a conclusion, being the predicate of the major premise.
(3) In the mnemonic names for the moodsof syllogism it signifies that the proposition denoted by the vowel after which this letter follows is, in the reduction to a direct mood, to be converted per accidens; as Baralipton, Felapton, Darapti. Such moods, from the Philonian point of view, are illogical. (C.S.P.) [253]
Paradox [Gr. παρά, contrary to, + δόξα opinion]: Ger. paradox (adj.); Fr. paradoxe; Ital. paradosso. An opinion surprising or repugnant to an ordinary mind. See De Morgan's Budget of Paradoxes. (C.S.P.) [258]
Parsimony (law of) [Lat. parsimonia, frugality]: Ger. Sparsamkeit; Fr. parcimonie; Ital. parsimonia. Ockham's razor, i.e. the maxim ‘Entia non sunt multiplicanda praeter necessitatem.’ The meaning is, that it is bad scientific method to introduce, at once, independent hypotheses to explain the same facts of observation.
Though the maxim was first put forward by nominalists, its validity must be admitted on all hands, with one limitation; namely, it may happen that there are two theories which, so far as can be seen, without further investigation, seem to account for a certain order of facts. One of these theories has the merit of superior simplicity. The other, though less simple, is on the whole more likely. But this second one cannot be thoroughly tested by a deeper penetration into the facts without doing almost all the work that would be required to test the former. In that case, although it is good scientific method to adopt the simpler hypothesis to guide systematic observations, yet it may be better judgment, in advance of more thorough knowledge, to suppose the more complex hypothesis to be true. For example, I know that men's motives are generally mixed. If, then, I see a man pursuing a line of conduct which apparently might be explained as thoroughly selfish, and yet might be explained as partly selfish and partly benevolent, then, since absolutely selfish characters are somewhat rare, it will be safer for me in my dealings with the man to assume the more complex hypothesis to be true; although were I to undertake an elaborate examination of the question, I ought to begin by ascertaining whether the hypothesis of pure selfishness would quite account for all he does. (C.S.P.) [264; CP 7.92-3]
Particular [Lat. particularis, singular]. In untechnical language, applied to single cases coming under general heads and occurring, or supposed to occur, in experience; in this sense it is also a substantive. The particulars are the experientially known circumstances of general nature, but as they appear in the individual case.
A particular PROPOSITION (q.v.) is one which gives a general description of an object and asserts that an object to which that description applies occurs in the universe of discourse, without asserting that it applies to the whole universe or to everything in the universe of a specified general description; as ‘Some dragons breathe fire.’ If we hold that the particular proposition asserts the existence of something, then the precise denial of it does not assert the existence of anything; as ‘No dragon breathing fire exists.’ It is, therefore, not true that from such precise denial any particular proposition follows, such as ‘Some dragon does not breathe fire.’ For if there is no dragon that does not breathe fire, this is false, although it may be true that there is no dragon that breathes fire. (C.S.P., C.L.F.) [CP 2.372]
This rule is not, of course, intended to apply to relative logic, in which there is frequently occasion to make a change from one copula to another—a change which is not contemplated in the ordinary logic. For instance, of the two propositions, ‘Some woman is adored by every Catholic,’ (Every Catholic adores some woman,’ the second follows from the first; to decide whether the first follows from the second or not, some further explicit convention as to the existence of terms which enter the proposition not as simple subject or predicate is necessary. (C.L.F.)
For instance, from the particular proposition, ‘Some woman is adored by all Catholics,’ it follows that ‘Any Catholic that may exist adores a woman,’ i.e., ‘There is no Catholic that does not adore a woman,’ which is the precise denial of ‘Some Catholic non-adores all women,’ which is a particular proposition. From this, in turn, it follows that a woman adored by all Catholics does not exist, which is the precise denial of the first proposition, ‘Some woman is adored by all Catholics.’ Of every particular proposition the same thing is true. Thus, if ‘Some crow is white,’ it follows that ‘No inevitable consequence of whiteness is wanting to all crows,’ which is the precise denial of the particular proposition, ‘Some inevitable consequence of whiteness is wanting in all crows.’ Thus, from every particular proposition follows the precise denial of a particular proposition, but from no precise denial of a particular proposition can any particular proposition follow. But this does not extend to a simple particular proposition, such as ‘Something is white,’ since to say ‘Something is non-existent’ (which the analogous treatment would yield) is an absurdity, and ought not to be considered as a proposition at all. (C.S.P., C.L.F.) [265-6, CP 2.373]
Particulate [Lat. particulatim, bit by bit. Particularis appears in Apuleius. Particulatio is used by Martianus Capella to mean breaking up into bits. Particulare and particulate are met with, not very often, in Albertus Magnus and others, to mean to particularize, particularized, whether in words or metaphysically of an essence] : (not in use in other languages). Particulate is used by recent writers chiefly in the sense of consisting of, or concerned with, particles. They appear to know nothing of the traditions of the word, but to have formed this adjective from particle, since particular bears a different meaning. (C.S.P.) [266]
Plurality of Causes: Ger. Mehrheit der Ursachen; Fr. pluralité des causes; Ital. pluralità delle cause. John Stuart Mill, in his System of Logic, III. v. 3, argues that ‘the cause, philosophically speaking, is the sum total of the conditions positive and negative taken together; the whole of the contingencies of every description, which being realized, the consequent invariably follows.’ This has been called the doctrine of ‘Plurality of Causes.’
This doctrine was not at all new when Mill's Logic was put forth. It had been the general view since the Aristotelian phraseology had been given up, and had even been common under the Aristotelian regime, although the word cause was then loaded down with many different meanings. But when Aristotelians used such phrases as the cause of a thing, or of an historical event—not of any fact, or abstract element of the event, expressible by a proposition, but of the whole event in its concreteness, such that no proposition, or book of propositions, or library of books of propositions, could begin to describe it adequately,—when Aristotelians used such phrases, of course they must mean something quite different by a cause, or efficient cause; and in fact we find that they fully recognized that any concrete thing or concrete event has multitudes of ‘efficient causes.’ In some cases they were able to mention one of these as the principalis efficiens. In other cases they spoke of one cause as being principalior than another. The Aristotelian doctrine did an incalculable amount of practical mischief, due to its utter confusion; and this confusion was owing to the attempt to give a meaning to the efficient cause of a concrete thing or concrete event.
Mill recognizes the enormous importance of clearing up the notion of cause. ‘The notion of cause,’ he says, ‘should be, with the utmost practicable degree of precision, fixed and determined.’ Nevertheless, so far is he from making his reader understand that the logical antecedent and consequent are not concrete things or events, but abstract elements thereof precisely and fully expressible by propositions, that after repeated re-readings of what he says, both in his Logic and elsewhere, one can but be left extremely doubtful whether Mill regarded the effect, or consequent, as a concrete event (he often says it is ‘an event’) or an abstract element of an event. He, and still more his followers, often seem to speak as if there were no single cause of an effect, in most cases. (C.S.P.)
It seems evident, however, that Mill—‘speaking philosophically,’ as he says—is not concerned with mere logical or abstract antecedence and consequence, but with the statement of the sum total of the conditions of a concrete event. Modern idealism puts the same truth, ‘philosophically speaking,’ in the doctrine that reality is a system the statement of which in its entirety is necessary for the statement of any part (fact, event, &c.) of it. See CAUSE AND EFFECT, and CAUSE AND CONDITION. (J.M.B., K.G.) [306-7]
Positive: [Lat. positum, from ponere, to place]: Ger. positiv; Fr. positif; Ital. positivo. (1) Logical: as applied to judgments, affirmative or asserting, opposed to negative or denying. Applied to terms, referring to a quality which is inherent, while a negative term connotes absence or limitation.
(2) Social and practical : that which depends upon will or convention instead of upon the forces of nature irrespective of human intervention; e. g. positive law, rights, religion, morality, &c. It is opposed to NATURAL (q. v.).
(3) Philosophical: that which depends upon observation of phenomena, or facts in space and time, not upon a thought process: the scientifically verifiable. Opposed to the speculative. See POSITIVISM. According to Comte, mankind passes through the theological and metaphysical stages in arriving finally at the positive. (J.D.)
Positive attribute: an experientially definite attribute, or one which for some other reason appears more definite than its contrary.
Positive denial: an explicit denial, opposed to one which is virtually made by an omission to affirm.
Positive discrepancy: a disagreement between statements consisting in the one asserting what the other positively denies. Positive distinction: a real distinction between two positively experimental objects, and not merely between an experience and the failure of it. There is a positive distinction between the odours of the rose and the orange-flower; a merely negative one between the perfume of the tea-rose and the want of perfume of the ordinary climber.
Positive idea: an idea due to a positive experience. Locke says: ‘Concerning the simple ideas of sensation, it is to be considered that whatsoever is so constituted in nature as to be able, by affecting our senses, to cause any perception in the mind, doth thereby produce in the understanding a simple idea; which, whatever be the external cause of it, when it comes to be taken notice of by our discerning faculty, it is by the mind looked on and considered there to be a real positive idea in the understanding, as much as any other whatsoever: though perhaps the cause of it be but a privation in the subject’ (Essay concerning Human Understanding, II. viii. i).
POSITIVE LAW (q. v.): a law laid down, a statute. ‘I would not here be mistaken, as if, because I deny an innate law, I thought there were none but positive laws’ (Locke, Essay concerning Human Understanding, I. iii. 13).
Positive philosophy (see POSITIVISM, also (3) above): the system of philosophy of Auguste Comte ; so called by him as composed of definite experiential results of science.
Positive proof or evidence: proof or evidence of a definite experience of the fact concluded. Positive proof is not necessarily more certain than negative proof. Thus, if a man comes home from business and finds all the portable valuables and his wife's best clothes gone, the wife having herself disappeared, this negative evidence that she took them is stronger than if a witness of suspicious character were to testify that she did so. Nor is positive proof or evidence the same as direct proof or evidence, as Kant and other writers say; for the fact that a man was in the utmost distress for want of money just after the robbery of a bank would be positive, yet indirect, evidence that he did not commit the robbery.
Positive proposition, judgment, or enunciation: a proposition more experientially definite in its assertion than its negative. An affirmative proposition is one which has the grammatical form of a positive proposition. But the present definition can only be regarded as tentative, since there has been no thorough investigation of the logical nature of the positiveness of propositions.
Positive whole: a whole made up of parts, in contradistinction to a whole indivisible even in thought, such as a person. (C.S.P.) [311-12]
Possibility, Impossibility, and Possible [Lat. possibile, from posse, may, can, be able; equivalent to the Gr. δυνατον]: Ger. Möglichkeit, Unmöglichkeit, möglich; Fr. possibilité, impossibilité, possible; Ital. possibilità, impossibilità, possibile.
[compiler's note: The first part of this article, down to the initials (J.D.), is apparently by John Dewey, and only the rest by Peirce; see the bracketed note at the end.]
The term is used to express a variety of meanings which, although distinct in themselves, yet flow readily into one another. These meanings may best be grouped according as they have (1) an ontological objective value, or a logical subjective value; and (2) according as they are used antithetically to actuality or necessity. The antithetical point of view is the most convenient from which to begin.
Possibility may mean that something is (1) not actual, or (2) that, while it possesses actual existence, that existence lacks causal or rational necessity.
(1) As opposed to the actual, the phrase has again a double meaning. (a) Taken objectively, it may mean something as yet undeveloped, since not presenting itself in actually objectified form, but capable of doing so at some future time, when all the conditions of its realization occur: latent, potential being. This implies capacity for realization; and, if this capacity be taken in an active sense, connotes some inherent tendency to actuality, which, if not thwarted, leads to final completeness of being. This involves the active sense of POTENTIALITY (q.v.), of FORCE (q.v.), &c. It is close to the literal sense of the term (posse, can be). This is the dominating sense in Greek philosophy, being connected with Aristotle's teleological theory of development. See NATURE, and POWER (δυναμις and ἐντελεχεια). (b) Taken logically, it denotes that there is some ground for asserting actuality, but not sufficient to justify a positive statement: may, as distinct from can, be. Thus, possibly it will rain tomorrow. It has to do with degrees of certainty in judging. See PROBABILITY.
(2) As opposed to the necessary, the term has also a double sense. (a) It may mean chance, contingency, as an objective fact. CHANCE (q.v.), again, has a double meaning: (i) something not derivable or explainable causally by reference to antecedent facts. There are those who assert the reality of such chance (see TYCHISM). On this view there are many possibilities in store in the future which no amount of knowledge would enable us to foresee or forestall. Indeterministic theories of the will assert possibilities of this sort also. (ii) Chance may mean that which, while necessary causally, is not necessary teleologically; the unplanned, the fatalistic. From this point of view the ‘possible’ is that which unexpectedly prevents the carrying-out of a purpose or intention. It leads up to the logical sense (b), according to which the possible, as opposed to the necessary, is anything whose existence cannot be derived from reason; that, the existence of which, rationally speaking, might be otherwise. It is opposed to mathematical or metaphysical necessity, where existence cannot be otherwise than as it is. In this sense the objective actual may be only (logically) possible; the present rain-storm is actual, but since it does not follow from a necessity of thought, but only from empirical antecedents, it is not necessary, and hence just a contingent possibility. This distinction goes back also to Aristotle, being found in his logical writings, as the possible, as potential meaning, is found in his metaphysical. It has played a large part in modern RATIONALISM (q.v.), especially in the philosophy of Leibnitz, being identical with his distinction of ‘truths of reason’ and ‘truths of fact.’ In the sphere of mathematics, logic, and metaphysics there is no possibility in the strict sense; all that exists exists of necessity. In the physical and practical spheres which deal with the space and time world the notion of possibility has full sway. Everything is possible which does not contradict the laws of reason; that which is inconceivable, which violates the law of reason, is impossible. The impossible is the self-contradictory. Kant's criticism of rational conceivability as a criterion of truth, to the effect that it is only formal, resting upon the principle of identity and contradiction, and when applied to existence must be supplemented by appeal to sense, made Leibnitz's distinctions of hardly more than historic interest.
The problems regarding the possible as a category of philosophy may be summed up as follows: Does it have any objective existence, or is it simply an expression of a certain logical attitude? If the former, is the objective possibility a necessary phase of a process of development, which will unfold itself into actuality; or does it express a particular fact, the reality of chance? If of logical significance only, does it flow from the distinction between a priori reason and a posteriori experience; or does it express a certain combination of ignorance and assurance in relation to facts, so that real possibilities would also be experienced facts? (J.D.)
The nominalistic definition (nominalistic in its real character, though generally admitted by realists, as Scotus, i. dist. 7, qu. unica) that that is possible which is not known not to be true in a real or assumed state of information is, like many nominalistic definitions, extremely helpful up to a certain point, while in the end proving itself quite superficial. It is not that certain things are possible because they are not known not to be true, but that they are not known not to be true because they are, more or less clearly, seen to be possible.
For example, one collection may be said to be greater than another if, and only if, there is no possible relation in which every member of the former collection stands to a member of the latter, to which no other member of the former stands in the same relation. Now, the question arises—whether or not it is possible for two collections to be, under this definition, each greater than the other. In advance of an investigation, the proposition is possibly true, in the sense that we do not know that it is impossible. But is the fact possible? That is, can we in any way suppose such a state of things without involving ourselves in contradiction? It is that positive supposition which will constitute the possibility, not the mere ignorance of whether such a supposition can be made or not. In order to make two such collections possible, we must make some positive assumption in regard to the possibility of collections; while in order to make such a relation between two collections impossible, we have to make a positive assumption of the possibility of a certain description of relation. It is not a question of ignorance, since nothing but pure hypothesis is concerned. The question is whether it is possible in every case to suppose distinct pairs, each composed of a member of either collection and such as completely to exhaust one of the collections. If this is always possible, then two collections each greater than the other are impossible. It is evidently desirable to state the logical principles of this general kind of possibility, which does not consist in ignorance, but, as it would seem, in hypothetic indetermination or disjunctive determination.
Nominalists uniformly speak of Aristotle's view of future contingents as really absurd. It may be so; but it is certainly the only doctrine which their principles leave room for. A certain event either will happen or it will not. There is nothing now in existence to constitute the truth of its being about to happen, or of its being about not to happen, unless it be certain circumstances to which only a law or uniformity can lend efficacy. But that law or uniformity, the nominalists say, has no real being; it is only a mental representation. If so, neither the being about to happen nor the being about not to happen has any reality at present; and the most that we can say is that the disjunction is true, but neither of the alternatives. If, however, we admit that the law has a real being, not of the mode of being of an individual, but even more real, then the future necessary consequent of a present state of things is as real and true as that present state of things itself.
By the old logicians, possibility is usually defined as non-repugnancy to existence. Kant defines it as that which satisfies the formal conditions of experience (Krit. d. Reinen Vernunft, 1st ed., 218, 234).
The possible proposition, or problematic judgment, as it is called by German logicians, is said by many logicians, especially Sigwart, not to be any proposition at all, because it does not draw a sharp line between truth and falsity. It seems to be necessary to distinguish between a proposition which asserts that under such and such general conditions a certain thing is possible, of which an example is the proposition that of any two collections one is not greater than the other, and a proposition which pretends to be no more than a conjecture. If a conjecture can be absolutely baseless, which may be doubted, a proposition which pretended to be no more than that may be said to be no proposition at all. But it can hardly be maintained that, when Poincaré says that there is no physical law whatever which will not be rendered more certain by every new confirmatory experiment, he is depriving those laws of all meaning as propositions.
Logical possibility: that of a hypothesis not involving any self-contradiction.
Mere possibility: that of a state of things which might come to pass, but, in point of fact, never will. In common language, exaggerated to the ‘merest possibility.’
Metaphysical possibility ought to mean a possibility of existence, nearly a potentiality; but the phrase does not seem to be used in that sense, but rather in the sense of possibility by supernatural power.
Moral possibility one might expect should be the opposite of moral impossibility, meaning, therefore, something reasonably free from extreme improbability. But, in fact, it seems to be used to mean what is morally permissible.
Physical possibility: (1) that which a knowledge of the laws of nature would not enable a person to be sure was not true; (2) that which might be brought about if psychological and spiritual conditions did not prevent, such as the Pope's pronouncing ex cathedra as an article of faith the fallibility of all his own utterances.
Practical possibility: that which lies within the power of a person or combination of persons under external conditions likely to be fulfilled, and questionable chiefly because internal conditions may not be fulfilled.
Proximate possibility. It is very difficult to make out what is meant by this; but the phrase is evidently modelled on potentia proxima, which is a state of high preparedness for existence; so that proximate possibility would be a high grade of possibility in a proposition amounting almost to positive assertion.
Real possibility is possibility in the thing, as contradistinguished from mere logical possibility (Scotus, Opus Oxon., I. ii. 7, Ad secundam probationem maioris).
Remote possibility: the possibility of a proposition which is far from being positively asserted. Also used in common speech.
Substantive possibility: the admissibility of a pure hypothesis (as illustrated above). (C.S.P.) [313-15; CP 6.364-71 —but note that the initials (J.D.) occurring halfway through the entry probably indicate that CP 6.364-7 is by John Dewey and not Peirce. The CP editors, however, omitted only the one paragraph which ends with Dewey's initials, presenting the rest as if it were all by Peirce.]
Postulate [Lat. postulatum, begged, used to translate Gr. αἴτημα] : Ger. Voraussetzung (the German Postulat = Forderung is a very different idea from that properly expressed by the French and English words); Fr. postulat; Ital. postulato. (1) The earliest definition we have of postulate, which was a technical term of Greek geometers, is by Aristotle. The passage has an appearance of incoherence; it is, however, plain that Aristotle makes a distinction between hypotheses and postulates which Euclid does not draw, and which is irrelevant. Omitting the distinction, the two have this in common—that they are propositions not necessarily true which are assumed as the bases of deductions.
If we turn to the first book of Euclid's Elements, we observe, in the first place, that he calls axioms by the name of common notions, a deliberate choice by him, for Aristotle, before his day, had called them axioms, though Aristotle usually calls them τὰ κοινά, nearly Euclid's name. These matters of common knowledge, according to Euclid's enumeration of them, are not specially geometrical, except that magnitudes superposable are equal (see the Cent. Dict., ‘Axiom’). On the other hand, the “postulates” of Euclid are all geometrical. They are as follows (according to the best MS. and all the evidence):—
(2) Since Wolff it has been very common among Germans, and among English writers who follow them, to define a postulate as an indemonstrable practical proposition. That is to say, it is an indemonstrable particular proposition, asserting that some general description of an object exists (in the only sense in which pure geometrical forms can be said to exist), in contradistinction to axioms, which were supposed to be indemonstrable theoretical (i.e. universal) propositions, asserting that some general description of an object has no existence as a geometrical form.
It is certainly desirable to have two terms bearing these meanings; but it was an utter misunderstanding to suppose that such were the proper meanings either of the word axiom or of the word postulate. The manner in which this misunderstanding came about is somewhat instructive. An axiom was a perfectly indubitable statement about things, in contradistinction to a definition, which cannot be called in question. On the contrary, a postulate was an indemonstrable proposition, not indubitable. There was some question whether certain postulates might not be considered to be axiomatic. When that was done, all the remaining postulates were particular propositions; namely, the first three of Euclid's list. This view was aided by the illogical notion that definitions could be considered as among the foundations of geometrical truth. Some writers went so far as to say that definitions were, or ought to be, the sole foundation of geometry—an extreme nominalistic position. But if definitions are allowed to take such a position, one postulate, at most, suffices, without any axiom; and all the rest of geometry can be thrown into a single definition. Namely, it is only necessary to postulate, say, that a point is possible, and to define a point in such a way as to make it cover the whole of geometry. This was not seen; and the practice of throwing geometrical truth over into definitions so far prevailed as to aid in restricting postulates to particular propositions. That such assumptions of possibility had a markedly different logical function from assumptions of impossibility was sufficiently clear to Wolff and the earlier writers whom he followed to cause him to put forth his definitions of axiom and postulate; and they recommended themselves all the more, because the postulates had become so familiar that it was no longer recognized that they were open to doubt.
(3) Kant calls his principles of modality “postulates of empirical thought” in the sense of judgments which are objectively analytical but subjectively synthetical. In fact, the principles as stated by him are not synthetical in any sense whatever, but are mere definitions. (C.S.P.) [313-15; CP 3.632-4]
Pragmatic (1) and (2) Pragmatism: [Gr. πραγματικος, versed in affairs]: Ger. pragmatisch, Pragmatismus; Fr. pragmatique, pragmatisme ; Ital. prammatico, prammatismo. (1) This term is applied by Kant to the species of hypothetical imperative which he otherwise denominates ‘counsel of prudence,’ and characterizes as ‘assertorial,’ those, namely, which prescribe the means necessary to the attainment of happiness, an end which we may postulate for all sentient beings (Grundlegung z. Met. d. Sitten, ed. Rosenkranz, 42; Eng. trans., Abbott, 34). (J.S.)
Pragmatic anthropology, according to Kant, is practical ethics.
Pragmatic horizon is the adaptation of our general knowledge to influencing our morals.
(2) The opinion that metaphysics is to be largely cleared up by the application of the following maxim for attaining clearness of apprehension: ‘Consider what effects, that might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object.’ (C.S.P.)
The doctrine that the whole ‘meaning’ of a conception expresses itself in practical consequences, consequences either in the shape of conduct to be recommended, or in that of experiences to be expected, if the conception be true; which consequences would be different if it were untrue, and must be different from the consequences by which the meaning of other conceptions is in turn expressed. If a second conception should not appear to have other consequences, then it must really be only the first conception under a different name. In methodology it is certain that to trace and compare their respective consequences is an admirable way of establishing the differing meanings of different conceptions. (W.J.)
This maxim was first proposed by C.S. Peirce in the Popular Science Monthly for January, 1878 (xii. 287); and he explained how it was to be applied to the doctrine of reality. The writer was led to the maxim by reflection upon Kant's Critic of the Pure Reason. Substantially the same way of dealing with ontology seems to have been practised by the Stoics. The writer subsequently saw that the principle might easily be misapplied, so as to sweep away the whole doctrine of incommensurables, and, in fact, the whole Weierstrassian way of regarding the calculus. In 1896 William James published his Will to Believe, and later his Philosophical Conceptions and Practical Results, which pushed this method to such extremes as must tend to give us pause. The doctrine appears to assume that the end of man is action—a stoical axiom which, to the present writer at the age of sixty, does not recommend itself so forcibly as it did at thirty. If it be admitted, on the contrary, that action wants an end, and that that end must be something of a general description, then the spirit of the maxim itself, which is that we must look to the upshot of our concepts in order rightly to apprehend them, would direct us towards something different from practical facts, namely, to general ideas, as the true interpreters of our thought. Nevertheless, the maxim has approved itself to the writer, after many years of trial, as of great utility in leading to a relatively high grade of clearness of thought. He would venture to suggest that it should always be put into practice with conscientious thoroughness, but that, when that has been done, and not before, a still higher grade of clearness of thought can be attained by remembering that the only ultimate good which the practical facts to which it directs attention can subserve is to further the development of concrete reasonableness; so that the meaning of the concept does not lie in any individual reactions at all, but in the manner in which those reactions contribute to that development. Indeed, in the article of 1878, above referred to, the writer practised better than he preached; for he applied the stoical maxim most unstoically, in such a sense as to insist upon the reality of the objects of general ideas in their generality.
A widely current opinion during the last quarter of a century has been that reasonableness is not a good in itself, but only for the sake of something else. Whether it be so or not seems to be a synthetical question, not to be settled by an appeal to the principle of contradiction—as if a reason for reasonableness were absurd. Almost everybody will now agree that the ultimate good lies in the evolutionary process in some way. If so, it is not in individual reactions in their segregation, but in something general or continuous. Synechism is founded on the notion that the coalescence, the becoming continuous, the becoming governed by laws, the becoming instinct with general ideas, are but phases of one and the same process of the growth of reasonableness. This is first shown to be true with mathematical exactitude in the field of logic, and is thence inferred to hold good metaphysically. It is not opposed to pragmatism in the manner in which C.S. Peirce applied it, but includes that procedure as a step. (C.S.P.)
It is of course legitimate to demand a reason for reasonableness; to do so is only to ask why we think—a question to which a genetic answer would seem to be afforded by certain forms of pragmatism. We may say (cf. SELECTION, in psychology) that reasonableness, or truth, is due to practical adjustments, and that the system of truths is developed by the selection of concrete relationships which ‘work.’ But it is quite another thing to make this genetic account of the origin and selection of ‘truth’ a philosophy of reality. For just the general or universal meaning of the system as a whole, the purpose or function which the concrete items selected as ‘workable’ subserves, and the environment or real world in which the entire movement takes place—all these are by definition outside the sphere of operation of pragmatism. Pragmatism is really an attempt to construe all reality ‘retrospectively’—as adequately given in the system of concrete practically derived truths—i.e. as empirical science; and while nominalism may invoke it, it still remains to prove nominalism. Cf. what is said under ORIGIN versus NATURE. In the words of Peirce (comment on this article): ‘Nominalism, up to that of Hegel, looks at reality retrospectively. What all modern philosophy does is to deny that there is any esse in futuro. Urban (Psychol. Rev., July, 1897) holds that while the concrete details of empirical knowledge may be due to ‘utility selection’—as practical ‘workables’—yet the structural principles of thought cannot be so accounted for. They have no application as generals, and so would have to the pragmatist no adequate ‘reason for being.’
The definition by W.J. above, however, seems, by including ‘experiences to be expected,’ to broaden the application of the principle.
Literature: besides the works of Peirce and James, as cited, see Caldwell, Pragmatism, in Mind, Oct., 1900; Miller, Philos. Rev., viii. (1899) 166; cf. Clifford, Lect. and Essays (1886), 85 ff. ; also the literature of SELECTIVE THINKING. (J.M.B.) [321-2, CP 5.1-4]
Precise [Lat. praecisus, abridged through Fr.]: Ger. präcis; Fr. précis; Ital. preciso. (1) Having that element of accuracy which consists in strict curtailment of superfluity. A precise narrative is one from which subjective interpolations have been rigidly excluded. A precise definition is one from which inessential characters are excluded. The definition of a circumference as an unterminated line in a plane, everywhere at the same distance from a point within, will be rendered precise by cutting off the word ‘within.’ In English the word is used more vaguely than in French.
(2) In physics it means having a very small error in consequence of the conscientious application of the most refined methods of measurement.
(3) In older writers the adjective is sometimes applied to a noun to signify that that noun is to be understood in its precise sense, without reference to accidental characters often associated with it. (C.S.P.) [323]
Precision [Lat. praecisio, through Fr.]: Ger. Präcision; Fr. précision (in all the senses of the English word; but in the technical logical sense it is obsolete in Fr.); Ital. precisione. (1) A high degree of approximation, only attainable by the thorough application of the most refined methods of science.
(2) Its earlier meaning, still more or less used by logicians, is derived from a meaning given to praecisio by Scotus and other scholastics: the act of supposing (whether with consciousness of fiction or not) something about one element of a percept, upon which the thought dwells, without paying any regard to other elements. Precision implies more than mere discrimination, which relates merely to the essence of a term. Thus I can, by an act of discrimination, separate colour from extension; but I cannot do so by precision, since I cannot suppose that in any possible universe colour (not colour-sensation, but colour as a quality of an object) exists without extension. So with triangularity and trilaterality. On the other hand, precision implies much less than dissociation, which, indeed, is not a term of logic, but of psychology. It is doubtful whether a person who is not devoid of the sense of sight can separate space from colour by dissociation, or, at any rate, not without great difficulty; but he can, and, indeed, does do so, by precision, if he thinks a vacuum is uncoloured. So it is, likewise, with space and tridimensionality.
Some writers called every description of abstraction by the name precision, dividing precision into the real and the mental, and the latter into the negative and the positive; but the better usage named these abstraction, divided into real and intentional, and the latter into negative (in which the character from which abstraction is made is imagined to be deniable of the subject prescinded) and into precisive abstraction or precision, where the subject prescinded is supposed (in some hypothetical state of things) without any supposition, whether affirmative or negative, in respect to the character abstracted. Hence, the brocard: abstrahentium non est mendacium (generally enunciated in connection with the De Anima, III. vii. 7). Scotus (in II. Physic., Expositio 20 textus 18) says: ‘Et si aliquis dicat, quod Mathematicis tune faciunt mendacium: quia considerant ista, quasi essent abstracta a motu, et materia; quae tamen sunt coniuncta materiae. Respondet, quod non faciunt mendacium: quia Mathematicus non considerat, utrum id, de quo demonstrat suas passiones, sit coniunctum materiae, vel abstractum a materia.’ This is not the place to treat of the many interesting logical, as well as psychological, discussions which have taken place concerning precision, which is one of the subjects which the scholastics treated in a comparatively modern way, although it leads directly to the question of nominalism and realism. It may, however, be mentioned that Scotus in many places draws a certain distinction variously designated by him and his followers (its nature and application is perhaps made as clear as anywhere in the Opus Oxon., III. xxii. qu. unica, ‘Utrum Christus fuerit homo in triduo,’ i.e. between the crucifixion and the resurrection), which the Thomists mostly dispute. There is some account of the matter in Chauvinus, Lexicon (2nd ed.), under ‘Praecisio.’
Hamilton has some remarks on the use of the words abstract and prescind, which could hardly come from any other man of equal learning and power, because no other such man is liable to be utterly confused by a slight complication. The remarks are mentioned here, because they have misled some students (Lects. on Met., xxxv; Lects. on Logic, vii). (C.S.P.) [323-4]
Predicament [the Eng. form of the Lat. praedicamentum, translating Gr. κατηγορια, category (Aristotle)] : Ger. Praedicament; Fr. catégorie; Ital. categoria. As a term of philosophy, predicament is exactly equivalent to CATEGORY (q.v.). Cf. Trendelenburg, Beitr. z. Logik; Baldwin, Handb. of Psychol., i. chap. xiv. § 4 ; Peirce, Proc. Amer. Acad. Arts and Sci., May, 1867. (C.S.P.) [325]
Predicate [Lat. praedicatum, from prae + dicare, to make public; used in Latin since Boethius, A.D. 500, in the logical sense. It was used by Boethius to translate κατηγορημα, κατηγορουμενον, or το ὁ of a proposition. Praedicatio, owing to its familiarity in the sense of preaching, was a little later in becoming a term of logic] : Ger. Prädicat; Fr. attribut, prédicat; Ital. predicato. (1) That element of a PROPOSITION (q. v.) which is brought into relation to the SUBJECT (q. v.). Cf. also JUDGMENT, and REASONING. (J.M.B.)
(2) The view which pragmatic logic takes of the predicate, in consequence of its assuming that the entire purpose of deductive logic is to ascertain the necessary conditions of the truth of signs, without any regard to the accidents of Indo-European grammar, will be here briefly stated. Cf. NEGATION.
In any proposition, i.e., any statement which must be true or false, let some parts be struck out so that the remnant is not a proposition, but is such that it becomes a proposition when each blank is filled by a proper name. The erasures are not to be made in a mechanical way, but with such modifications as may be necessary to preserve the partial sense of the fragment. Such a residue is a predicate. The same proposition may be mutilated in various ways so that different fragments will appear as predicates. Thus, take the proposition ‘Every man reveres some woman.’ This contains the following predicates, among others:
‘ _____ reveres some woman.’
‘ _____ is either not a man or reveres some woman.’
‘Any previously selected man reveres _____ .’
‘Any previously selected man is _____ .’
See NEGATION. (C.S.P.) [325-6, CP 2.358]
Predication [Lat. praedicare, to assert]: Ger. Aussage, Prädikation; Fr. attribution, détermination; Ital. affermazione.
[(1) In psychology (by G.F.S., J.M.B., C.L.F.)]
(2) In logic: the joining of a predicate to a subject of a PROPOSITION (q.v.) so as to increase the logical breadth without diminishing the logical depth.
On the relation between the psychological and the logical views of predication, see PROPOSITION (1).
This still leaves room for understanding predication in various ways, according to the conception entertained of the dissection of a proposition into subject and predicate. It is a question under dispute today whether predication is the essential function of the proposition. Some maintain that the proposition ‘It rains’ involves no predication. But if it is an assertion, it does not mean that it rains in fairyland, but the very act of saying anything with an appearance of seriously meaning it is an INDEX (q.v.) that forces the person addressed to look about to see what it is to which what is being said refers. The ‘rains’ recalls to his mind an image of fine up-and-down lines over the field of view; and he looks sharply out of the window, fully understanding that that visible environment is indicated as the subject where the lines of falling drops will be seen. In like manner, there is a predication in a conditional or other hypothetical proposition, in the same sense that some recognized range of experience or thought is referred to.
[article continued for one paragraph by C.L.F.]
A few of the most frequently recurring scholastic phrases follow.
Abstract predication: predication of a subject considered in the abstract.
Accidental predication: predication of an accident.
Analogical predication; a rather favourite expression of Aquinas: predication in which the predicate is taken neither in its strict sense nor in an unrelated sense, but in a peculiar sense for which there is a good reason, us when a statue is said to be a man.
Complete predication: predication in which the whole nature of the thing is formally affirmed.
Analogical predication; a rather favourite expression of Aquinas: predication in which the predicate is taken neither in its strict sense nor in an unrelated sense, but in a peculiar sense for which there is a good reason, as when a statue is said to be a man.
Denominative predication: predication in which that whose nature it is to be a subject is taken as the subject, and something whose nature it is to be predicated is taken as the predicate; a predication of an accident of a substance. (It is well discussed by Scotus, In univ. Porph., 9. 16, (Utrum haec sit vera, Homo est animalis,’ where, as in the majority of scholastic disputations, the conclusion is foregone, and the interest lies in the formidable difficulties and how they are to be overcome.) Denominative predication, in its proper sense, is predication of an accidental concrete term of its own subject; in a broad sense, it is the predication of any concrete of a suppositum, or of any subject of less breadth; in the widest sense, it is predication of any predicate of any subject. Denominative predication may be a posteriori or a priori, as homo est albus, rationale est substantia, homo est animal.
Determinative predication: same as denominative predication.
Dialectic predication, as defined by Aristotle (I. Top., x): the predication of a general term in a proposition which may result from an argument in a probable place, and not reducible to anything prior.
Direct predication: predication in the usual sense of representing that the breadth of the subject belongs to the predicate, and the depth of the predicate to the subject; or, in scholastic language, it is predication of a higher term of a lower one, of a passion of a subject, of an accident of a subject, of a mode of a quiddity, of a difference of a genus.
Equivocal predication: predication which may be taken in two unrelated senses.
Essential predication: in which the predicate is wholly contained in the essence of the subject. It is, therefore, in Kant's sense, an analytical judgment. But neither Kant nor the scholastics provide for the fact that an indefinitely complicated proposition, very far from obvious, may often be deduced by mathematical reasoning, or necessary deduction, by the logic of relatives, from a definition of the utmost simplicity, without assuming any hypothesis whatever (indeed, such assumption could only render the proposition deduced simpler); and this may contain many notions not explicit in the definition. This may be illustrated by the following: Man is a rational animal; hence, whatever is not a man is either, on the one hand, not rational, while either at the same time being an animal or else benefiting nothing except such objects as love nothing but fairies, or, on the other hand, is not an animal, while either being rational or standing to whatever fairy may exist in the relation of benefiting something that loves it. Now, if it be said that that is an analytical judgment, or essential predication, neither the definition of the scholastics nor that of Kant is adequate. But if it be said that it is not an essential predication, or analytical judgment, then the accidental predication and the synthetical judgment may be a necessary consequence, and a very recondite one, of a mere definition, quite contrary to what either Kant or the scholastics supposed and built upon. Cf. Scotus (In univ. Porph., 9. 12), who makes essential predication the predication of genus, species, or difference.
Exercised predication. The distinction between exercised and signate predication belongs to Scotus. (The passage which Prantl attributes to Antonius Andreas is a quotation verbatim from Scotus, as often naturally happens in Prantl's Geschichte.) A signate predication is one which is said to be made, an exercised predication is one which is made; so that Scotus says: ‘A praedicari signato ad praedicari exercitum non tenet consequentia per se in eisdem terminis.’ Scotus gives the following examples of the distinction, where the exercised predication is marked E, the signate S: S, Genus praedicatur de specie; E, Homo est animal. (The Lyons text here transposes the terms, which we give correctly.) S, nego; E, non. E, tantum; S, excludo. The abstract definition of Scotus is: ‘Esse in rebus primae intentionis illud exercet quod praedicari signat in secundis intentionibus.’ Exercised predication is distinguished into praedicatio de proprio supposito and praedicatio de subiecto; the former is essential, the latter accidental.
Formal predication: predication where the predicate is in the concept of the subject, independent of any extrinsic cause or of any particular matter in qua. The difference between formal and essential predication is somewhat trivial and confused.
Identical predication: the predication of a term of itself.
Incomplete predication: see complete predication.
Indirect predication has two meanings. In one sense, it might better be called relative predication, since it is the predication of some term which occurs in the predicate in an oblique case, as angles are predicated of triangles. But, in another sense, Chauvinus (Lexicon, 2nd ed., 1713, ‘Praedicatio’) says: ‘Praedicatio contra naturam, seu inordinata, quae alias etiam dicitur indirecta, ea est vel in qua inferius de superiori in eadem linea praedicamentali, aut id quod se habet per modum materiae de eo quod se habet per modum formae dicitur; … vel, in qua species de sua dicitur differentia … vel, in qua substantia dicitur de accidente connotativo.’ Mauritius Hibernicus, in his Expositio quaest. D. Subtilis in quinque Vniv. Porph., qu. i. art. 31, says, ‘Voco communiter praedicationem directam,’ and proceeds to give substantially the definition of Chauvinus.
Inordinate predication: see quotation from Chauvinus under Indirect predication.
Intrinsic predication: one in which the predicate is in the subject independently of the relations of the latter to other things.
Natural predication: when the subject and predicate ought to be so related according to their nature. This is substantially the definition given in many books; but it conveys little idea of how the expression is used. Natural predication is always divided into the identical and direct; non-natural predication is either indirect, i.e., contra naturam, or it is praeter naturam, i.e., per accidens. Examples of indirect predication, where the subject is related to the predicate as form to matter, are alba est nix, animal est homo. Examples of predication praeter naturam, where subject and predicate are related to some third term, as form to matter, are album est dulce, dulce est album. Examples of direct predication: nix est alba, homo est animal. Examples of identical predication: gladius est ensis, Plato est Plato (Conimbricenses in Praef. Porph., q.i. art. 4).
Non-natural predication: see Natural predication.
Proper predication: a predication in which the verb and predicate are taken in their proper signification.
Qualificative predication: see Predication in quale.
Quidditative predication: see Predication in quid.
Signate predication: see Exercised predication.
Univocal predication: predication of a univocal term.
Predication de omni is defined by Aristotle in the dictum de omni; that is, what is predicated of a subject universally, or de omni, is predicated of everything of which that subject is predicated.
Predication in eo quod quid (translation of ἐν τῷ τί ἐστι κατηγορεῖσθαι) occurs in the translation of the Isagoge by Marius Victorinus, and means predication of the genu and species. In some of the late scholastics it is distinguished from other predication in quid, and is confined to predication of the genus (see Eckius, In Petr. Hisp.). But others, as the Mainz doctors, retain the earlier meaning.
Predication in eo quod quale: same as predication in quale, from which, however, some of the later writers discriminate it.
Predication in quale, as most commonly used, is predication of difference, property, or accident. But it is also, not infrequently, restricted to predication of the property or accident. Albertus Magnus (In predicabilibus, tr. iii. cap. iv) distinguishes four different senses of predication in quale.
Predication in quale quid: predication of a specific difference.
Predication in quid (the expression appears in the 12th century. It is an abbreviation of in eo quod quid). Used in a number of senses, for which see any good mediaeval logic; and especially for predication of the genus and species, most strictly of the latter.
Predication per accidens: see Natural predication.
Predication per causam: a predication that the predicate stands in a causal relation to the subject.
Predication per comitantiam or concomitantiam: a predication that the predicate accompanies the subject.
Predication per essentiam: essential predication.
Predication per se: see PER SE.
Predication quasi in quid = in quale quid.
(C.S.P.) [326-9, CP 2.359-61]
Predicative Proposition. The old name for a categorical PROPOSITION (q. v., also CATEGORICAL), used by Apuleius, Marcianus Capella, and Boethius. Cassiodorus, however, has categoricus, which was used by Abelard and subsequent logicians. The expression has been revived by some modern logicians who do not think that all propositions, nor even all categorical propositions, such as ‘It rains,’ predicate anything. (C.S.P.) [329]
Premise (and Premiss) [two distinct words, recognized as such by older writers, but for the last century and more confounded. Premise is a legal word, derived from the French prémise, which is a noun derived from the phrase les choses prémises, used in inventories. Premiss is from the French noun prémisse, and thence from the Low Lat. praemissa, which goes back, as a substantive, to the early part of the thirteenth century. But it was hardly looked upon as a very good Latin at any time. Propositio replaced it, when elegance was preferred to technical accuracy] : Ger. Vordersatz, Prämisse; Fr. prémisse; Ital. premessa. A proposition, the consideration of which has logically affected, or contributed to the determination of, a conclusion of reasoning.
An enthymeme is usually defined as a syllogism with a suppressed premise or premiss. Now, the expression of a train of thought may be elliptical, some thought being unexpressed in the confident anticipation that the reader, or hearer, will supply it. But in thought, a premise or premiss cannot be suppressed without ceasing to be either premise or premiss. If it be so suppressed, it enters into the leading principle of the inference. Every reasoning must proceed consciously upon some general principle, or it ceases to be a reasoning, and becomes a mere feeling of inability to think otherwise. On the other hand, when a principle of reasoning becomes by analysis distinctly apprehended and the precise effect which it has upon the conclusion understood, it becomes a premise, or, at least, a premiss. There is, therefore, no such thing as a suppressed premiss.
The word premiss became usual in the logical sense, in English, as early as Chaucer. In Wilson's Rule of Reason (1552) it does not occur, the phraseology there being like the following: ‘The double repeate, whiche is a woorde rehearsed in bothe Proposicions, must not entre into the conclusion.’ But in Blundevile's Arte of Logicke (1599) we read: ‘A Syllogisme is a kinde of argument contayning three Propositions, whereof the two first, commonly called the premisses,’ &c. In Watts's and other English logics it was spelt premiss and premisses. Johnson, however, in his Dictionary, gives premises in the plural and premiss in the singular, as distinct words, and remarks that the latter is little used in the plural outside of technical works. In such works the word spelt with two s's continued to be employed. (C.S.P.) [CP 2.582-3]
The two forms of spelling, for the logical term, are used interchangeably in this work. (J.M.B.) [330-1]
Presupposition [Lat. prae + suppositus, placed under] : Ger. Voraussetzung; Fr. présupposition (a coined word); Ital. presupposto. Presupposition is either a conjecture or what is better called in English a POSTULATE (q. v.).
As a philosophical term it translates the German Voraussetzung, and is presumably preferred to ‘postulate’ by Germans and others imperfectly acquainted with the English language, because they suppose that postulate in English has the same meaning as Postulat in German, which is not true; for the English retains the old meaning, while the German has generally adopted the conception of Wolff. If postulate does not exactly translate German Voraussetzung, it comes, at any rate, quite as near to doing so as presupposition; a good translation would be ‘assumption.’ (C.S.P.) [338, CP 3.635]
Probable Inference: Ger. Wahrscheinlichkeitsschluss; Fr. inférence probable; Ital. illazione probabile. Any inference which does not regard its own conclusion as being necessarily true (though the facts be as the premisses assert).
In such an inference the facts asserted in the premisses are regarded as constituting a sign of the fact stated in the conclusion in one or other of three senses, as follows: i.e., that relation of the premissed facts to the concluded fact which is regarded as making the former a sign of the latter (1) may be such as could not exist until the conclusion was problematically recognized; this is inductive or experimental inference. Such a relation (2) may be altogether irrespective of whether the conclusion is recognized or not, yet such that it could not subsist if the concluded fact were not probable; this is probable deduction. Such a relation (3) may consist merely in the premissed facts having some character which may agree with, or be in some other relation to, a character which the concluded fact would possess if it existed; this is presumptive inference.
(1) The first case is that in which we begin by asking how often certain described conditions will, in the long run of experience, be followed by a result of a predesignate description; then proceeding to note the results as events of that kind present themselves in experience; and finally, when a considerable number of instances have been collected, inferring that the general character of the whole endless succession of similar events in the course of experience will be approximately of the character observed. For that endless series must have some character; and it would be absurd to say that experience has a character which is never manifested. But there is no other way in which the character of that series can manifest itself than while the endless series is still incomplete. Therefore, if the character manifested by the series up to a certain point is not that character which the entire series possesses, still, as the series goes on, it must eventually tend, however irregularly, towards becoming so; and all the rest of the reasoner's life will be a continuation of this inferential process. This inference does not depend upon any assumption that the series will be endless, or that the future will be like the past, or that nature is uniform, nor upon any material assumption whatever. Cf. INDUCTION, and UNIFORMITY OF NATURE.
Logic imposes upon us two rules in performing this inference. The first is this: so far as in us lies, the conditions of the experience should remain the same. For we are reasoning exclusively from experience, that is, from the cognitions which the history of our lives forces upon us. So far as our will is allowed to interfere, it is not experience; so we must take pains that we do not, in taking the instances from which we are to reason, restrict the conditions or relax them from those to which the question referred. The second prescription of logic is that the conclusion be confined strictly to the question. If the instances examined are found to be remarkable in any other respect than that for which they were selected, we can draw no inference of the present kind from that. It would be merely an infinitely weaker inference of the third kind (below). The present kind of inference derives its great force from the circumstance that the result is virtually predicted.
(2) The second kind of probable inference is, by the definition of it, necessary inference. But necessary inference may be applied to probability as its subject-matter; and it then becomes, under another aspect, probable inference. If of an endless series of possible experiences a definite proportion will present a certain character (which is the sort of fact called an objective probability), then it necessarily follows that, foreseen or not, approximately the same proportion of any finite portion of that series will present the same character, either as it is, or when it has been sufficiently extended. This is governed by precisely the same principle as the inductive inference, but applied in the reverse way. The same prescriptions of logic apply as before; but, owing to that being now inferred which was in the other case a premiss, and conversely, it is not here true that the relation of the facts laid down in the premisses to the fact stated in the conclusion, which makes the former significant of the latter, requires the recognition of the conclusion. This is probable deduction. It covers all the ordinary and legitimate applications of the mathematical doctrine of PROBABILITY (q.v.).
The legitimate results of the calculus of probability are of enormous importance, but others are unfortunately vitiated by confusing mere likelihood, or subjective probability, with the objective probability to which the theory ought to be restricted. An objective probability is the ratio in the long run of experience of the number of events which present the character of which the probability is predicated to the total number of events which fulfill certain conditions often not explicitly stated, which all the events considered fulfill. But the majority of mathematical treatises on probability follow Laplace in results to which a very unclear conception of probability led him. Laplace and other mathematicians, though they regard a probability as a ratio of two numbers, yet, instead of holding that it is the limiting ratio of occurrences of different kinds in the course of experience, hold that it is the ratio between numbers of ‘cases,’ or special suppositions, whose ‘possibilities’ (a word not clearly distinguished, if at all, from ‘probabilities’) are equal in the sense that we are aware of no reason for inclining to one rather than to another. This is an error often appearing in the books under the head of ‘inverse probabilities’ (see that subject under PROBABILITY, where the view of Laplace is criticized).
(3) Probable inference of the third kind includes those cases in which the facts asserted in the premisses do not compel the truth of the fact concluded, and where the significant observations have not been suggested by the consideration of what the consequences of the conclusion would be, but have either suggested the conclusion or have been remarked during a search in the facts for features agreeable or conflicting with the conclusion. The whole argument then reduces itself to this, that the observed facts show that the truth is similar to the fact asserted in the conclusion. This may, of course, be reinforced by arguments of some other kind; but we should begin by considering the case in which it stands alone. As an example to fix ideas, suppose that I am reading a long anonymous poem. As I proceed, I meet with trait after trait which seems as if the poem were written by a woman. In what way do the premisses justify the acceptance of that conclusion, and in what sense? It does not necessarily, nor with any necessitated objective probability, follow from the premisses; nor must the method eventually lead to the truth. The only possible justifications which it might have would be that the acceptance of the conclusion or of the method might necessarily conduce, in the long run, to such attainment of truth as might be possible by any means, or else to the attainment of some other purpose. All these alternatives ought to be carefully examined by the logician in order that he may be assured that no mode of probable inference has been overlooked.
It appears that there is a mode of inference in which the conclusion is accepted as having some chance of being true, and as being at any rate put in such a form as to suggest experimentation by which the degree of its truth can be ascertained. The only method by which it can be proved that a method, without necessarily leading to the truth, has some tolerable chance of doing so, is evidently the empirical, or inductive, method. Hence, as induction is proved to be valid by necessary deduction, so this presumptive inference must be proved valid by induction from experience.
The presumptive conclusion is accepted only problematically, that is to say, as meriting an inductive examination. The principal rule of presumption is that its conclusion should be such that definite consequences can be plentifully deduced from it of a kind which can be checked by observation. Among the wealth of methods to which this kind of inference (perhaps by virtue of its experiential origin) gives birth, the best deserving of mention is that which always prefers the hypothesis which suggests an experiment whose different possible results appear to be, as nearly as possible, equally likely.
Among probable inferences of mixed character, there are many forms of great importance. The most interesting, perhaps, is the argument from ANALOGY (q.v.), in which, from a few instances of objects agreeing in a few well-defined respects, inference is made that another object, known to agree with the others in all but one of those respects, agrees in that respect also. (C.S.P.) [353-5; CP 2.783-7]
Quality (in grammar and logic.) (1) Take a sentence in which a common noun or adjective is predicated of a proper noun, and imagine that there is something in the reality which corresponds to the form of the proposition. Then imagine that this form of fact consists in a relation of the objective subject, or substance, to one being, the same correlate for all cases where the same noun or adjective is predicated in the same sense, and that imaginary being, whether looked upon as real, or merely as a convenience of thought, is a quality. Thus, if anything is beautiful, white or incomprehensible, this consists in its possessing the quality of beauty, whiteness, or incomprehensibility.
(2) But in a more proper sense the term quality will not be applied when the adjective, like incomprehensible, is conceived as signifying a relation. Thus, whiteness will be, in this narrow sense, a quality only so long as objects are thought as being white independently of anything else; but when this is conceived as a relation to the eye, ‘whiteness’ is only a quality in a looser sense. Locke defines quality as the power of producing an idea, which agrees with the above explanation tolerably.
Qualitas, having inevitably reached an excessively vague use, was in the Roman schools taken to designate almost any character or characters for which no other name was at hand. Thus arose a variety of special senses. Thus in grammar the difference between nouns which had a plural and those which had not was called a difference of quality; as was the difference between the personal pronouns and qui, quis, &c.
(3) In logic: the distinction between the affirmative and the negative PROPOSITION (q.v.) has been called the distinction of quality in propositions by all logicians, without interruption, from Apuleius, in the 2nd century of our era, to our own contemporaries.
Kant, in order to round out a triad, added a third quality, called LIMITATIVE (q.v., 1), that of ‘Sortes est non homo,’ with a distinction from ‘Sortes non est homo.’ This will not bear criticism; but Kant's authority and the force of tradition have caused it to survive. As long as the universe of characters is unlimited, it is obvious that any collection of objects have some predicate common and peculiar to them. This being the case, as ordinary syllogistic tacitly assumes it is, the distinction between affirmative and negative propositions is purely relative to the particular predicate. No doubt many logicians have assumed that negative propositions are distinguished from ordinary affirmative propositions in not implying the reality of the subject. But what, then, does ‘Some patriarch does not die’ mean? Besides, all admit that propositions per se primo modo do not imply the existence of the subject, although they be affirmative. At any rate, the resulting syllogistic, if consistent, is very objectionable. If, however, the universe of characters is limited, as it is in ordinary speech, where we say that logical inconsistency and mandarin oranges have nothing in common, then the system of formal logic required will be a simple case of the logic of RELATIVES (q.v.); but the distinction of affirmative and negative propositions will become material or absolute, the forms of simple categorical propositions then being:
Any A possesses every character of the group β.
Any A wants every character of the group β.
Any A possesses some character of the group β.
Any A wants some character of the group β.
Some A possesses every character of the group β, &c.
(4) Quality, even in Aristotle, is especially employed to denote characters which constitute merits or demerits; and this word is remarkable for the number of specialized meanings that it bears. Since Kant it has been employed to designate the distinction of clear and obscure, or distinct and confused, &c. See the preceding topic.
Quality is distinguished as primary, secondary, secundo-primary, essential or substantial, accidental, manifest, occult, primitive, original, elementary, first, derived, real, intentional, imputed, passible, logical, propositional, active, alterant, affective, predicamental, &c. (C.S.P.) [408-9; CP 2.374-7]
Quantity (in logic and mathematics). (1) Any ACCIDENT (q.v.) whereby a substance has part outside of part. Cf. QUANTITY (2).
This is the old definition; and it is true to the old meaning of the word in representing quantity as much more concrete than the modern conception. Quantity (see Aristotle's Praedicamenta, vi) is either discrete or continuous. Continuous quantity is either magnitude or time. The old definition of mathematics as the science of quantity is misunderstood, if quantity is here taken in the modern sense; it was only meant that mathematics treated of accidents having number, magnitude, or duration. There was therefore a mathematics of music.
(2) In the general modern sense, quantity is a system of serial relationships.
Serial relationship differs from transitive relationship merely in the point of view, and (so closely connected are the two points of view) in hardly more than the mode of expression. Now, all transitive relation is traceable to inclusion. Hence, quantity might be defined as a system of inclusions looked upon as serial. It is very important to understand that quantity is a mere system of relative ordinal relations in a linear series. Each complete determination of quantity in a given system is a ‘value.’
Quantity is either counted or measured. Counted quantity may have a finite multitude of values. Of systems of quantity of denumeral multitude, the simplest is that of the integer numbers. The system of rational fractions is the only other familiarly used. These fractions can, in several ways, be arranged in their order of quantity by mere counting.
(3) Concepts, or terms, are, in logic, conceived to have subjective parts, being the narrower terms into which they are divisible, and definitive parts, which are the higher terms of which their definitions or descriptions are composed: these relationships constitute ‘quantity.’
This double way of regarding a class-term as a whole of parts is remarked by Aristotle in several places (e.g., Met., Δ. xxv. 1023 b 22). It was familiar to logicians of every age. Thus Scotus Erigena calls logic ‘ars illa quae diuidit genera in species et species in genera resoluit.’ John of Salisbury refers to the distinction as ‘quod fere in omnium ore celebre est, aliud scilicet esse quod appellativa [i.e. adjectives and the like] significant, et aliud esse quod nominant. Nominantur singularia, sed universalia significantur.’ For William of Auvergne, see Prantl, iii. 77. The writer has a long list of similar passages before him. But the Aristotelians had their minds upon the discrimination of different kinds of predication, and insisted that the differences of different genera are different, thus forbidding cross-divisions. Arnauld, however, in l'Art de penser, conceives all predicates, or all essential predicates, as alike, without distinguishing genus and differentia; and was so led to devote a short chapter (vi) to l'étendue and la compréhension before taking up the predicables. But his services in the matter have been grossly exaggerated, and it really seems to have been Kant who made these ideas pervade logic and who first expressly called them quantities. But the idea was old. Archbishop Thomson, W. D. Wilson, and C. S. Peirce endeavor to make out a third quantity of terms. The last calls his third quantity ‘information,’ and defines it as the ‘sum of synthetical propositions in which the symbol is subject or predicate,’ antecedent or consequent. The word ‘symbol’ is here employed because this logician regards the quantities as belonging to propositions and to arguments, as well as to terms. A distinction of extensive and comprehensive distinctness is due to Scotus (Opus Oxon., I. ii. 3): namely, the usual effect upon a term of an increase of information will be either to increase its breadth without diminishing its depth, or to increase its depth without diminishing its breadth. But the effect may be to show that the subjects to which the term was already known to be applicable include the entire breadth of another term which had not been known to be so included. In that case, the first term has gained in extensive distinctness. Or the effect may be to teach that the marks already known to be predicable of the term include the entire depth of another term not previously known to be so included, thus increasing the comprehensive distinctness of the former term. The passage of thought from a broader to a narrower concept without change of information, and consequently with increase of depth, is called descent; the reverse passage, ascent. For various purposes, we often imagine our information to be less than it is. When this has the effect of diminishing the breadth of a term without increasing its depth, the change is called restriction; just as when, by an increase of real information, a term gains breadth without losing depth, it is said to gain EXTENSION (q.v., in logic). This is, for example, a common effect of induction. In such case, the effect is called GENERALIZATION (q.v.). A decrease of supposed information may have the effect of diminishing the depth of a term without increasing its information. This is often called abstraction; but it is far better to call it prescission; for the word abstraction is wanted as the designation of an even far more important procedure, whereby a transitive element of thought is made substantive, as in the grammatical change of an adjective into an abstract noun. This may be called the principal engine of mathematical thought. When an increase of real information has the effect of increasing the depth of a term without diminishing the breadth, the proper word for the process is amplification. In ordinary language, we are inaccurately said to specify, instead of to amplify, when we add to information in this way. The logical operation of forming a hypothesis often has this effect, which may, in such case, be called supposition. Almost any increase of depth may be called determination.
(4) Syllogistic is sometimes regarded as the mathematics of a system of quantities consisting of but two values, truth and falsity.
(5) The quantity of a proposition is that respect in which a universal proposition is regarded as asserting more than the corresponding particular proposition: the recognized quantities are UNIVERSAL, PARTICULAR, SINGULAR (see those terms, in logic), and—opposed to these as ‘definite’—Indefinite. Quantitas is used in this sense by Apuleius.
Quantification of the Predicate. The attachment of signs of propositional quantity to the predicates of simple propositions is called by this name. The dictum de omni defines the relation of subject and predicate, so that ‘Any A is B’ is to be understood as meaning ‘To whatever A is applicable, B is applicable.’ But this definition must be modified, in order to give any room for a quantification of the predicate. If then we are to take all and some in their proper distributive senses and not in collective senses, to say that ‘Every man is every animal’ would, as Aristotle remarks, be absurd, unless it were meant that there was but one man and one animal, and that that one man was identical with that one animal. This system has never been proposed. But Hamilton, with his followers, T. S. Baynes and Calderwood, take the marks of quantity in a collective sense. They thus have, as one of the propositional forms, ‘Some man is not some animal,’ which precisely denies ‘Every man is every animal,’ in the distributive sense, and is entitled to an equal standing in logic. It does not deny ‘All man is all animal,’ in the collective sense of these logicians. This system had some vogue in its day.
De Morgan's system of Propositions. This permits the retention of the dictum de omni, merely applying propositional quality to the subject. We thus get the following eight forms of proposition:
)) To whatever A is applicable, B is applicable.
(·) To whatever A is inapplicable, B is applicable.
)·( To whatever A is applicable, B is inapplicable.
(( To whatever A is inapplicable, B is inapplicable; i.e. To whatever B is applicable, A is applicable.
() To something to which A is applicable, B is applicable.
(·( To something to which A is applicable, B is inapplicable.
)·) To something to which A is inapplicable, B is applicable; i.e., To something to which B is applicable, A is inapplicable.
)( To something to which A is inapplicable, B is inapplicable.
The above is substantially one of De Morgan's own forms of statement, called by him onymatic. There is no objection to this system; but it is an idle complication of forms which does not enable us to take account of any mode of inference that the old system does not cover. Still it does away with the figures of syllogism. But whatever the merits or demerits of the system, De Morgan developed it with logical elegance. (C.S.P.) [410-12; CP 2.362-6]
Reasoning: Ger. Schliessen (inference), Denken (thought); Fr. raisonnement; Ital. ragionamento. Thinking in logical form, correct or incorrect.
‘Direct’ reasoning or inference is the case in which the proof proceeds directly to the conclusion ; an ‘indirect’ conclusion follows from the proof of something else (see PROOF). ‘Deceptive reasoning’ is reasoning which involves a logical fallacy. (J.M.B.)
Reasoning is a process in which the reasoner is conscious that a judgment, the conclusion, is determined by other judgment or judgments, the premises, according to a general habit of thought, which he may not be able precisely to formulate, but which he approves as conducive to true knowledge. By true knowledge he means, though he is not usually able to analyse his meaning, the ultimate knowledge in which he hopes that belief may ultimately rest, undisturbed by doubt, in regard to the particular subject to which his conclusion relates. Without this logical approval, the process, although it may be closely analogous to reasoning in other respects, lacks the essence of reasoning. Every reasoner, therefore, since he approves certain habits, and consequently methods, of reasoning, accepts a logical doctrine, called his logica utens. Reasoning does not begin until a judgment has been formed; for the antecedent cognitive operations are not subject to logical approval or disapproval, being subconscious, or not sufficiently near the surface of consciousness, and therefore uncontrollable. Reasoning, therefore, begins with premises which are adopted as representing percepts, or generalizations of such percepts. All the reasoner's conclusions ought to refer solely to the percepts, or rather to propositions expressing facts of perception. But this is not to say that the general conceptions to which he attains have no value in themselves.
Reasoning is of three elementary kinds; but mixed reasonings are more common. These three kinds are induction, deduction, and presumption (for which the present writer proposes the name abduction).
Induction takes place when the reasoner already holds a theory more or less problematically (ranging from a pure interrogative apprehension to a strong leaning mixed with ever so little doubt); and having reflected that if that theory be true, then under certain conditions certain phenomena ought to appear (the stranger and less antecedently credible the better), proceeds to experiment, that is, to realize those conditions and watch for the predicted phenomena. Upon their appearance he accepts the theory with a modality which recognizes it provisionally as approximately true. The logical warrant for this is that this method persistently applied to the problem must in the long run produce a convergence (though irregular) to the truth; for the truth of a theory consists very largely in this, that every perceptual deduction from it is verified. It is of the essence of induction that the consequence of the theory should be drawn first in regard to the unknown, or virtually unknown, result of experiment; and that this should virtually be only ascertained afterward. For if we look over the phenomena to find agreements with the theory, it is a mere question of ingenuity and industry how many we shall find. Induction (at least, in its typical forms) contributes nothing to our knowledge except to tell us approximately how often, in the course of such experience as our experiments go towards constituting, a given sort of event occurs. It thus simply evaluates an objective probability. Its validity does not depend upon the uniformity of nature, or anything of that kind. The uniformity of nature may tend to give the probability evaluated an extremely great or small value; but even if nature were not uniform, induction would be sure to find it out, so long as inductive reasoning could be performed at all. Of course a certain degree of special uniformity is requisite for that.
But all the above is at variance with the doctrines of almost all logicians; and, in particular, they commonly teach that the inductive conclusion approximates to the truth because of the uniformity of nature. They only contemplate as inductive reasoning cases in which, from finding that certain individuals of a class have certain characters, the reasoner concludes that every single individual of the class has the same character. According to the definition here given, that inference is not inductive, but is a mixture of deduction and presumption. Cf. INDUCTION, and PROBABLE INFERENCE.
On the methods of inductive reasoning see DIFFERENCE (method of), CONCOMITANCE (logical), AGREEMENT (method of), and Elimination under SCIENTIFIC METHOD. For Eliminative Reasoning (Ausschlussverfahren—Eisler) see SYLLOGISM.
Presumption, or, more precisely, abduction (which the present writer believes to have been what Aristotle's twenty-fifth chapter of the second Prior Analytics imperfectly described under the name of ἀπαγωγη, until Apellicon substituted a single wrong word and thus disturbed the sense of the whole), furnishes the reasoner with the problematic theory which induction verifies. Upon finding himself confronted with a phenomenon unlike what he would have expected under the circumstances, he looks over its features and notices some remarkable character or relation among them, which he at once recognizes as being characteristic of some conception with which his mind is already stored, so that a theory is suggested which would explain (that is, render necessary) that which is surprising in the phenomena.
He therefore accepts that theory so far as to give it a high place in the list of theories of those phenomena which call for further examination. If this is all his conclusion amounts to, it may be asked: What need of reasoning was there? Is he not free to examine what theories he likes? The answer is that it is a question of economy. If he examines all the foolish theories he might imagine, he never will (short of a miracle) light upon the true one. Indeed, even with the most rational procedure, he never would do so, were there not an affinity between his ideas and nature's ways. However, if there be any attainable truth, as he hopes, it is plain that the only way in which it is to be attained is by trying the hypotheses which seem reasonable and which lead to such consequences as are observed.
Presumption is the only kind of reasoning which supplies new ideas, the only kind which is, in this sense, synthetic. Induction is justified as a method which must in the long run lead up to the truth, and that, by gradual modification of the actual conclusion. There is no such warrant for presumption. The hypothesis which it problematically concludes is frequently utterly wrong itself, and even the method need not ever lead to the truth; for it may be that the features of the phenomena which it aims to explain have no rational explanation at all. Its only justification is that its method is the only way in which there can be any hope of attaining a rational explanation. This doctrine agrees substantially with that of some logicians; but it is radically at variance with a common theory and with a common practice. This prescribes that the reasoner should be guided by balancing probabilities, according to the doctrine of inverse PROBABILITY (q. v.). This depends upon knowing antecedent probabilities. If these antecedent probabilities were solid statistical facts, like those upon which the insurance business rests, the ordinary precepts and practice would be sound. But they are not and cannot, in the nature of things, be statistical facts. What is the antecedent probability that matter should be composed of atoms? Can we take statistics of a multitude of different universes? An objective probability is the ratio of frequency of a specific to a generic event in the ordinary course of experience. Of a fact per se it is absurd to speak of objective probability. All that is attainable are subjective probabilities, or likelihoods, which express nothing but the conformity of a new suggestion to our prepossessions; and these are the source of most of the errors into which man falls, and of all the worst of them. An instance of what the method of balancing likelihoods leads to is the higher criticism of ancient history, upon which the archaeologist's spade has inflicted so many wounds. Cf. PRESUMPTIVE INFERENCE.
The third elementary way of reasoning is deduction, of which the warrant is that the facts presented in the premises could not under any imaginable circumstances be true without involving the truth of the conclusion, which is therefore accepted with necessary modality. But though it be necessary in its modality, it does not by any means follow that the conclusion is certainly true. When we are reasoning about purely hypothetical states of things, as in mathematics, and can make it one of our hypotheses that what is true shall depend only on a certain kind of condition—so that, for example, what is true of equations written in black ink would certainly be equally true if they were written in red—we can be certain of our conclusions, provided no blunders have been committed. This is ‘demonstrative reasoning.’ Fallacies in pure mathematics have gone undetected for many centuries. It is to ideal states of things alone—or to real states of things as ideally conceived, always more or less departing from the reality—that deduction applies. The process is as follows, at least in many cases:
We form in the imagination some sort of diagrammatic, that is, iconic, representation of the facts, as skeletonized as possible. The impression of the present writer is that with ordinary persons this is always a visual image, or mixed visual and muscular; but this is an opinion not founded on any systematic examination. If visual, it will either be geometrical, that is, such that familiar spatial relations stand for the relations asserted in the premises, or it will be algebraical, where the relations are expressed by objects which are imagined to be subject to certain rules, whether conventional or experiential. This diagram, which has been constructed to represent intuitively or semi-intuitively the same relations which are abstractly expressed in the premises, is then observed, and a hypothesis suggests itself that there is a certain relation between some of its parts—or perhaps this hypothesis had already been suggested. In order to test this, various experiments are made upon the diagram, which is changed in various ways. This is a proceeding extremely similar to induction, from which, however, it differs widely, in that it does not deal with a course of experience, but with whether or not a certain state of things can be imagined. Now, since it is part of the hypothesis that only a very limited kind of condition can affect the result, the necessary experimentation can be very quickly completed; and it is seen that the conclusion is compelled to be true by the conditions of the construction of the diagram. This is called ‘diagrammatic or schematic, reasoning.’
Literature : F. A. LANGE, Logische Stud. (1877, unfinished); J. S. MILL, A System of Logic (1842); treatises on logic generally; many treatises on psychology, in loc.; BIBLIOG. C, 2, j, k. (C.S.P.) [426-8; CP 2.773-8]
Relatives (logic of) : Ger. logische Beziehungslehre; Fr. logique des relations (L.C.); Ital. termini relativi. If from any proposition having more than one subject (used to include ‘objects’) we strike out the indices of the subjects, as in ‘― praises ― to ―,’ ‘― dat in matrimonium ―,’ what remains and requires at least two insertions of subject-nouns to make a proposition is a ‘relative term,’ or ‘relative rhema,’ called briefly a ‘relative.’ The relative may be converted into a complete assertion by filling up the blanks with proper names or abstract nouns; this serves as a criterion.
But in such a relative there must be such an idea of the difference between the subjects to be applied that ‘dat in matrimonium’ shall be different from ‘datur in matrimonium.’ In order to free ourselves from the accidents of speech, we might represent the sentence by the following diagram:

Relatives may be more or less general like other terms, that is, one relative may be predicable of members of a set of which another is not, while the latter is predicable only of members of sets of which the former is predicable. By a set is meant an ordered system, so that ABC and BCA, though the same collection, are different sets. As any general term is predicable of any one of an aggregate of individuals, so a relative is predicable of any one of an aggregate of sets; and each such set may be regarded as an individual relative. By a system is meant an individual of which if anything is true, the truth of it consists in certain things being true of certain other individuals, called its members, regardless of the system. A system is either a sorite, heap, or mere collection, or it is a set. A sorite is a system of which, if anything is true, its truth consists of the truth of one predicate for any one of the members. A set is a system of which the truth of anything consists in the truth of different predicates. Of course the idea of relation is involved in the idea of a system. As it is very important for the understanding of relations that the conception of a system should be perfectly clear, let us consider the latter a moment in its simplest form, that of a sorite or mere collection. ABC is a sorite. Thus, it is true of it that it contains the three first letters of the alphabet, and the truth of that consists in A, B, and C being each one of the first three letters of the alphabet. It is true that it contains nothing but the first letters of the alphabet, because it is true of A, B, C severally that each is nothing but one of the first three letters of the alphabet. AB is a different sorite, because something is true of it which is not true of ABC. A may be regarded as a sorite provided we mean not A in its first intention and being, but a something whose being consists in A's being. The collection A is not the letter A, but it contains A and nothing else. If it be said that there is no such thing, the reply is that every collection, every system may be said to be an ens rationis. To this point we shall return. Even Nothing may be said to be a collection. For when we say that Nothing is less than 1, we do not mean that a self-subsisting individual is so, but that an ens rationis whose mode of being consists in the absence of everything is less than 1. The sorite ABC is other than ABΓ. But should I say that ABC contains two of the letters of Caesar's first name, and subsequently learn that that was a mistake, the real name being Gaius, that would not make ABC a different sorite.
That in the reality which corresponds to a proposition with a relative predicate is called the fundamentum relationis. A relationship is a system of such fundamenta. Relation is the relative character, conceived as belonging in different ways to the different relates, and (owing to the somewhat undue prominence given by familiar languages to one of these) especially to the relate which is denoted by the noun which is the subject nominative.
Relatives and relations are said to differ in their orders, according to the numbers of their relates. Dyadic or dual relations, or relatives of two relates, of which the second is called the correlate, differ somewhat widely from plural, or polyadic, relations. Triadic relations have all the principal characters of tetradic and higher relations. In fact, a compound of two triadic relatives may be a tetradic relative; as ‘praiser of ― to a maligner of ― to ―.’
Relatives may be compounded in all the ways in which other terms can be compounded as well as in other ways closely related to those. Thus, A may be said to be at once a lover and a servant of B, and it may be said that there is something, X, such that A is a lover of X, while X is a servant of B; so that A is a lover of a servant of B. This mode of composition is called relative multiplication. So, not only may it be said that A is either a lover or a servant of B (not excluding both), but also that whatever X may be, either A is a lover of X or X is a servant of B; that is, A is a lover of everything there is besides servants of B. (This wording, by Schröder, slightly violates English idiom, but is valuable as showing the analogy to aggregation.) This mode of composition is called relative addition. So, again, it may not only be said that A is if a lover then a servant of B, but also that whatever X may be, if A is a lover of X, then X is a servant of B; that is, A is a lover only of servants of B. This is called relative regressive involution. Or it may be said that whatever X may be, A is a lover of X, if X is a servant of B, or A is a lover of whatever is a servant of B. This is called relative progressive involution. Polyadic relatives are capable of other modes of composition. Thus, it may be said that anything whatever, X, being taken, something Y exists, such that A praises X to Y while X maligns Y to B; that is, A praises everybody to somebody maligned by him to B. Or we can say that there is something, Y, such that, whatever X may be, A praises X to Y while X maligns Y to B; or, A praises everybody to somebody whom everybody maligns to B.
Deductive logic can really not be understood without the study of the logic of relatives, which corrects innumerable serious errors into which not merely logicians, but people who never opened a logic-book, fall from confining their attention to non-relative logic. One such error is that demonstrative reasoning is something altogether unlike observation. But the intricate forms of inference of relative logic call for such studied scrutiny of the representations of the facts, which representations are of an iconic kind, in that they represent relations in the fact by analogous relations in the representation, that we cannot fail to remark that it is by observation of diagrams that the reasoning proceeds in such cases. We successively simplify them and are always able to remark that such observation is required, and that it is even thus, and not otherwise, that the conclusion of a simple syllogism is seen to follow from its premisses. Again, non-relative logic has given logicians the idea that deductive inference was a following out of a rigid rule, so that machines have been constructed to draw conclusions. But this conception is not borne out by relative logic. People commonly talk of the conclusion from a pair of premisses, as if there were but one inference to be drawn. But relative logic shows that from any proposition whatever, without a second, an endless series of necessary consequences can be deduced; and it very frequently happens that a number of distinct lines of inference may be taken, none leading into another. That this must be the case is indeed evident without going into the logic of relatives, from the vast multitude of theorems deducible from the few incomplex premisses of the theory of numbers. But ordinary logic has nothing but barren sorites to explain how this can be. Since Kant, especially, it has been customary to say that deduction only elicits what was implicitly thought in the premisses; and the famous distinction of analytical and synthetical judgments is based upon that notion. But the logic of relatives shows that this is not the case in any other sense than one which reduces it to an empty form of words. Matter entirely foreign to the premisses may appear in the conclusion. Moreover, so far is it from being true, as Kant would have it, that all reasoning is reasoning in Barbara, that that inference itself is discovered by the microscope of relatives to be resolvable into more than half a dozen distinct steps. In minor points the doctrines of ordinary logic are so constantly modified or reversed that it is no exaggeration to say that deductive logic is completely metamorphosed by the study of relatives.
One branch of deductive logic, of which from the nature of things ordinary logic could give no satisfactory account, relates to the vitally important matter of abstraction. Indeed, the student of ordinary logic naturally regards abstraction, or the passage from "the rose smells sweet" to "the rose has perfume," to be a quasi-grammatical matter, calling for little or no notice from the logician. The fact is, however, that almost every great step in mathematical reasoning derives its importance from the fact that it involves an abstraction. For by means of abstraction the transitory elements of thought, the ἔπεα πτερόεντα, are made substantive elements, as James terms them, ἔπεα ἀπτερόεντα. It thus becomes possible to study their relations and to apply to these relations discoveries already made respecting analogous relations. In this way, for example, operations become themselves the subjects of operations.
To take a most elementary example — from the idea of a particle moving, we pass to the idea of a particle describing a line. This line is then thought as moving, and so as generating a surface; and so the relations of surfaces become the subject of thought. An abstraction is an ens rationis whose being consists in the truth of an ordinary predication. A collection, or system, is an abstraction or abstract ens; and thus the whole doctrine of number is founded on the operation of abstraction. If we conceive an object to be a collective whole, but to be so in such a way that it has no part which is not itself a collective whole in the same way, then, if the collection is of the nature of a sorite, it is a general, whose parts are distinguished merely as having additional characters; but if the collection is a set, whose members have other relations to one another, it is a continuum. The logic of continua is the most important branch of the logic of relatives, and mathematics, especially geometrical topic, or topical geometry, has its developement retarded from the lack of a developed logic of continua.
Literature: relatives have, since Aristotle, been a recognized topic of logic. The first germ of the modern doctrine appears in a somewhat trivial remark of Robert Leslie Ellis. De Morgan did the first systematic work in his fourth memoir on the syllogism in 1860 (Cambridge Philosophical Transactions, x. 331-358); he here sketched out the theory of dyadic relations. C. S. Peirce, in 1870, extended Boole's algebra so as to apply to them, and after many attempts produced a good general algebra of logic, together with another algebra specially adapted to dyadic relations (Studies in Logic, by members of the Johns Hopkins University, 1883, Note B, 187-203). Schröder developed the last in a systematic manner (which brought out its glaring defect of involving hundreds of merely formal theorems without any significance, and some of them quite difficult) in the third volume of his Exakte Logik (1895). Schröder's work contains much else of great value. PEIRCE has published only three papers since 1883, one of which appeared in the Amer. J. of Math., vii. (1885) 180-202, and the other two in the Monist. vii. (1896-7) 19-40, 161-217. An important work in which relations are treated graphically is A. B. KEMPE'S Theory of Mathematical Form, published in the Philos. Trans. for 1890. Other workers are JOSEPH JOHN MURPHY, ALEXANDER MACFARLANE, GlUSEPPE PEANO, GEORG CANTOR, RICHARD DEDEKIND, and others have treated relations of quantity, and their writings—especially DEDEKIND'S book, Essays on the Theory of Number (Eng. trans., 1901) are particularly recommended to students of philosophy. Translations of parts of some of CANTOR'S memoirs into most puzzling French are given in the Acta Mathematica, ii; the Math. Annalen (xlvi and xlix) contain others of great importance; and CANTOR especially addresses students of philosophy in his Zur Lehre vom Transfiniten Erste Abth.,(1890). This brochure consists of papers originally printed in the Zeitsch. f. Philos. u. philos. Krit. See also V. B. RUSSELL, Sur la logique des relations, in Revue de Mathématiques, vii (1901); WHITEHEAD, in recent numbers of the Amer. J. of Math. (C.S.P.) [447-450; CP 3.636-643]
Remote [Lat. remotus, from re + movere, to move] : Ger. zurückliegend ; Fr. éloigné ; Ital. rimoto. The older word for which mediate has of late been generally substituted. See IMMEDIATE AND MEDIATE. So in the phrases ‘remote object,’ ‘remote mark,’ ‘remote scibile,’ ‘remote witness.’ The opposite of remote is proximate. (C.S.P.)
Remote cause : that which produces an effect (remote) through or with the production of another effect (proximate). (J.M.B.)
In law, remote cause is an act of which the agent is not responsible for the remote effects.
Remote matter, (1) In Aristotelian metaphysics: matter relatively less prepared for the reception of a given form, by having received accidents or by substantial forms. (2) In logic : the matter of matter. Thus, terms are the remote matter of syllogisms, being the matter of propositions, which are the proximate matter. (3) In the doctrine of the matter of propositions which we find in the Summulae, remote matter consists of terms of a proposition which, from the nature of their significates, cannot either of them be true of the other. (C.S.P.) [463]
Represent [Lat. re + praesentare, to present] : Ger. Repräsentiren; Fr. représenter; Ital. rappresentare. To stand for, that is, to be in such a relation to another that for certain purposes it is treated by some mind as if it were that other.
Thus a spokesman, deputy, attorney, agent, vicar, diagram, symptom, counter, description, concept, premiss, testimony, all represent something else, in their several ways, to minds who consider them in that way. See SIGN. When it is desired to distinguish between that which represents and the act or relation of representing, the former may be termed the ‘representamen,’ the latter the ‘representation.’ (C.S.P.) [464, CP 2.273]
Representationism : Ger. Repräsentationismus; Fr. représentationisme; Ital. rapresentazionismo. The doctrine that percepts stand for something behind them. See COSMOTHETIC IDEALISM, and IDEALISM.
In a certain sense it must be admitted, even by presentationists, that percepts only perform the function of conveying knowledge of something else. That is to say, they have to be combined and generalized to become useful knowledge; so that they may be said to represent their own generalizations. In this, representationists and presentationists may agree. But the dispute between them consists in this, that the representationist regards the percept in the light of testimony or a picture, from which by inference, or a mental act analogous to inference, the hidden cause of the percept may become known; while the presentationist holds that perception is a two-sided consciousness in which the percept appears as forcibly acting upon us, so that in perception the consciousness of an active object and of a subject acted on are as indivisible as, in making a muscular effort, the sense of exertion is one with and inseparable from the sense of resistance. The representationist would not allow that there is any bilateral consciousness even in the latter sense, regarding the bilaterality as a quasi-inference, or product of the mind's action; while the presentationist insists that there is nothing intellectual or intelligible in this duality. It is, he says, a hard fact experienced but never understood. A representationist will naturally regard the theory that everything in the outward world is atoms, their masses, motions, and energy, as a statement of the real fact which percepts represent. The presentationist, on the other hand, will more naturally regard it as a formula which is fitted to sum up and reconcile the percepts as the only ultimate facts. These are, however, merely different points of view in which neither ought to find anything absolutely contrary to his own doctrine. (C.S.P.) [464-5, CP 5.607]
Scientific Method : [Ger. wissenschaftliche Methode; Fr. méthode scientifique; Ital. metodo scientifico. The general method of successful scientific research. The following are some of its characteristics. Cf. Science.
(1) The student's first step is to form a perfectly definite and consistent idea of what the problem really is; then he ought to develop the mathematics of the subject in hand as far as possible; and to establish a mathematical method appropriate to the particular problem, if it be one which allows exact treatment. As examples and models of what is meant, may be mentioned Maxwell's researches on colour sensation in the Philos. Trans. for 1860, Flinders Petrie's book Inductive Metrology, the last chapters of Pearson's Grammar of Science. Of course, as the student's understanding of the matter advances, he will return to this first task, and continually improve upon his first essays.
The second step will be to consider the logic and methodeutic of the research in hand, unless it is itself a question of pure mathematics, where the logic is inseparable from the mathematics. He will do well to study the manner in which questions somewhat analogous to his own have been successfully resolved in widely different fields; for the greatest advantage has accrued from the extension of methods from one subject to a widely different one, especially from simple to intricate matters.
The third step should be to reform his metaphysics, if the question is a broad one. Perhaps he thinks he has no metaphysics, and does not wish to have any. That will be a sure sign that he is badly handicapped with metaphysics of the crudest quality. The only way to disburden himself of it is to direct his attention to it. But he cannot reduce himself to anything like absolute scepticism in metaphysics without arresting his work.
The fourth step will be to study the laws of the phenomena dealt with, so far as they can be made out at this stage. The general order of discovery in the nomological sciences is first to pick up the phenomena by excursions in those fields in which they are to be found, with alertness of observation, with those clear ideas that make the new fact instantly recognizable as new, and with the energy that seizes upon the faint trace and follows it up. Witness the manner in which all the new phenomena of radiation have been brought to light during the last generation: cathode rays, X rays, Becquerel rays, etc. After making some acquaintance with the phenomena, the next discovery is of their laws (nomological). In the light of one's metaphysics and general conception of the department of truth dealt with, one considers what different hypotheses have any claims to investigation. The leading considerations here will be those of the 'economics' of research. If, for example, a hypothesis would necessitate an experimental result that can be cheaply refuted if it is not true, or would be greatly at variance with preconceived ideas, that hypothesis has a strong claim to early examination. But one must not give up a hypothesis too readily. Many a discovery has been missed by that fault. Gravitation would have been known a decade earlier if Newton had not hastily thought it refuted, and so set back all the subsequent history of physics by something like that amount of time lost. It is likely that thousands of persons more will die of consumption — as remote as that may seem — than would have died if he had not made that error. The testing of the hypothesis proceeds by deducing from it experimental consequences almost incredible, and finding that they really happen, or that some modification of the theory is required, or else that it must be entirely abandoned. The law of the phenomena once made out, it only remains to measure with precision the values of the coefficients in the equation which expresses it.
The problem under investigation may not be of a nomological kind. Not that the phenomena are not conceivably subject to law, so that the subject may ultimately be received into the nomological sciences,— as chemistry, for example, promises some day to mature into a nomological science; but in the present state of knowledge the question, we will suppose, cannot be so studied. Still, a certain amount of nomological study is a necessary preliminary to engaging with the problem itself. Biology calls for aid from physiology. The student who is studying the growth of languages must avail himself of all the knowledge that there is about the physics of speech sounds. In case, then, the question has not yet reached the nomological stage, the sixth step in the work will be of a classificatory nature. Such order, of a more or less imperfect kind, as can be traced in the phenomena must be made out. Students of the classificatory sciences like to call such regularities laws. The tendency is a symptom of health; because it shows that law is their ideal, and that they are striving to bring their sciences to the nomological stage. But such orderlinesses as ‘Grimm's Law’ (see Gender) and ‘Mendeléef's Law’ are not laws in the sense in which the association of ideas and the three laws of motion are laws. They are not satisfactory for a minute. They are nothing that can blend with our metaphysics; they are not of a universal kind; and they are not precise. You may imagine that there might be a chain of more and more universal, precise, and reasonable regularities leading from these to those. But there is, in fact, a great gap, which has to be acknowledged. A hypothesis may be made about the cause of the three laws of motion; but we can have no present hopes of satisfactorily proving the truth of such a thing; while we at once set to work with great hopes of making considerable steps towards explaining Mendeléef's Law and Grimm's Law. But the most important distinction between true laws and such regularities lies in the very different way in which we proceed to the discovery of the one and of the other. The whole attitude of mind is so different that it is difficult to believe that the same man would have great success in the two tasks. We have seen in our day the establishment of a grand example of each kind, the Law of the Conservation of Energy (q.v.) and the Periodic Law. The one dealt with a small number of observations. Exactitude was the main thing. The hypothesis itself sprang almost immediately from the natural light of reason. In the other case, it was necessary with a positive effort to put ideas of exactitude aside and to find order in a great tangle of facts.
Perhaps the problem in hand relates to one of those sciences basely called descriptive, that is, sciences which study, not classes of facts, but individual facts, such as history, descriptive astronomy, geography. No science is merely descriptive. These sciences are investigations of causes. The historian's facts of observation are not those contained in his text, but those mentioned in the foot-notes — the documents and monuments. It is the supposed causes of these which make the text. Nor is he contented with a mere chronicle of striking public events; he endeavours to show what the hidden causes of them were. So the astronomer's real business is to prove the Nebular Hypothesis (q.v.) or whatever ought to replace it. The geologist does not merely make a geological map, but shows how the existing state of things must have come to pass. To do this the historian has to be a profound psychologist, the geologist a master of physics and dynamics. Just as the classificatory sciences tend to become nomological, so the descriptive, or explanatory, sciences tend to become classificatory. The astronomer finds so many examples of systems in formation, that he can formulate the cycle of events through which they generally pass; as the historian formulates cycles through which communities usually pass, and the geologist formulates cycles through which continents commonly pass. These are analogous to the cyclical laws of the classificatory sciences.
But perhaps the problem before the student is not one of theoretical physics or of theoretical psychics, but a practical problem. He wishes to invent. In that case he ought to have a great knowledge both of facts about men's minds and of facts about matter; for he has to adapt the one to the other. He ought to know more than any pure scientist can be expected to know. Of course, as the world goes, he does not.
(2) The most vital factors in the method of modern science have not been the following of this or that logical prescription — although these have had their value too — but they have been the moral factors. First of these has been the genuine love of truth and conviction that nothing else could long endure. Given that men strive after the truth, and, in the nature of things, they will get it in a measure. The greatest difference between the scientific state of the modern scientific era from Copernicus and the middle ages, is that now the whole concern of students is to find out the truth; while then it was to put into a rational light the faith of which they were already possessed. The chief obstacle to the advance of science among students of science in the modern era has been that they were teachers, and feared the effect of this or that theory. But the salvation from this danger has been the fact that there was no vast institution which anybody for a moment hoped could withstand the mighty tide of fact. The next most vital factor of the method of modern science is that it has been made social. On the one hand, what a scientific man recognizes as a fact of science must be something open to anybody to observe, provided he fulfils the necessary conditions, external and internal. As long as only one man has been able to see a marking upon the planet Venus, it is not an established fact. Ghost stories and all that cannot become the subject of genuine science until they can in some way be welded to ordinary experience. On the other hand, the method of modern science is social in respect to the solidarity of its efforts. The scientific world is like a colony of insects, in that the individual strives to produce that which he himself cannot hope to enjoy. One generation collects premises in order that a distant generation may discover what they mean. When a problem comes before the scientific world, a hundred men immediately set all their energies to work upon it. One contributes this, another that. Another company, standing upon the shoulders of the first, strike a little higher, until at last the parapet is attained. Still another moral factor of the method of science, perhaps even more vital than the last, is the self-confidence of it. In order to appreciate this, it is to be remembered that the entire fabric of science has to be built up out of surmises at truth. All that experiment can do is to tell us when we have surmised wrong. The right surmise is left for us to produce. The ancient world under these circumstances, with the exception of a few men born out of their time, looked upon physics as something about which only vague surmises could be made, and upon which close study would be thrown away. So, venturing nothing, they naturally could gain nothing. But modern science has never faltered in its confidence that it would ultimately find out the truth concerning any question in which it could apply the check of experiment.
These are some of the more vital factors of the method of modern science. For the purely logical elements the reader should consult special topics, e.g. Reasoning, Probable Inference, Psychophysical Methods, Errors of Observation, Empirical Logic, Variation, &c. (C.S.P., J.M.B.) [500-503; CP 7.79-88]
Sign [Lat. signum, a mark, a token] : Ger. Zeichen; Fr. signe; Ital. segno. (1) Anything which determines something else (its interpretant) to refer to an object to which itself refers (its object) in the same way, the interpretant becoming in turn a sign, and so on ad infinitum.
No doubt, intelligent consciousness must enter into the series. If the series of successive interpretants comes to an end, the sign is thereby rendered imperfect, at least. If, an interpretant idea having been determined in an individual consciousness, it determines no outward sign, but that consciousness becomes annihilated, or otherwise loses all memory or other significant effect of the sign, it becomes absolutely undiscoverable that there ever was such an idea in that consciousness; and in that case it is difficult to see how it could have any meaning to say that that consciousness ever had the idea, since the saying so would be an interpretant of that idea.
A sign is either an icon, an index, or a symbol. An icon is a sign which would possess the character which renders it significant, even though its object had no existence; such as a lead-pencil streak as representing a geometrical line. An index is a sign which would, at once, lose the character which makes it a sign if its object were removed, but would not lose that character if there were no interpretant. Such, for instance, is a piece of mould with a bullet-hole in it as sign of a shot; for without the shot there would have been no hole; but there is a hole there, whether anybody has the sense to attribute it to a shot or not. A symbol is a sign which would lose the character which renders it a sign if there were no interpretant. Such is any utterance of speech which signifies what it does only by virtue of its being understood to have that signification.
(2) Used for COEFFICIENT (q. v.) or MARK (q. v.). Cf. LOCAL SIGN, and TEMPORAL SIGN. (C.S.P.) [527-8, CP 2.303-4]
This division of signs, suggested by C.S.P., may be compared with the more generally recognized classification given under SIGN-MAKING FUNCTION [by G.F.S., 529-30]; they serve different purposes, and do not seem to be inconsistent. (J.M.B.)
Signification (and Application, in logic): Ger Bedeutung; Fr. signification; Ital. significato. See CONNOTATION (2), and DENOTATION, and cf. MEANING, SIGNIFICS, and SEMANTICS.
These are substitute terms for what are called by Mill and others connotation and denotation; for (1) the previously well-established use of connote was somewhat warped by Mill and his followers, and (2) these words may be applied to the corresponding properties of propositions as well as terms. The application of a term is the collection of objects which it refers to; of a proposition it is the instances of its holding good. The ‘signification’ of a term is all the qualities which are indicated by it; of a proposition it is all its different implications.
Great confusion has arisen in logic from failing to distinguish between the different sorts of signification, or connotation, of a term: thus to the question, Are proper names connotative? ‘contradictory answers are given by ordinarily clear thinkers as being obviously correct,’ for the reason that they have not the same thing in mind under the term connotation. It is necessary to distinguish between (1) the indispensable signification; (2) the banal signification; (3) the informational signification; and (4) the complete signification. (1) is so much as is contained in whatever may be fixed upon as the definition of the term—all those elements of the meaning in the absence of any one of which the name would not be applied; (2) is what ‘goes without saying,’ what is known to every one, and (3) is what there is occasion to give utterance to: these of course vary with the different individuals to whom the proposition is given out—that oxygen is exhilarating is informational to the student of chemistry, and banal to the teacher of chemistry (but false to those who are familiar with the latest results of the science); (4) consists of all the valid predicates of the term in question. When I say, ‘The one I saw yesterday was John Peter,’ the indispensable signification of John Peter is simply an individual object of consciousness (usually a man, though it may be a dog, or a doll) whom it has been agreed to designate by that name; but the banal signification, to one who knows John Peter well, is very extensive.
The same characteristics apply to propositions as well as to terms: thus the complete signification (or implication) of All x is y is all its valid consequences, and its complete application (or range) is all those descriptions of circumstances under which it holds good—that is to say, all its sufficient antecedents. (C.L.F., C.S.P.)
A general term denotes whatever there may be which possesses the characters which it signifies; J. S. Mill uses, in place of signifies, the term connotes, a word which he or his father picked up in Ockham. But signify has been in uninterrupted use in this sense since the 12th century, when John of Salisbury spoke of ‘quod fere in omnium ore celebre est, aliud scilicet esse appellativa significant, et aliud esse quod nominant. Nominantur singularia; sed universalia significantur.’ Nothing can be clearer. There is no known occurrence of connote as early as this. Alexander of Hales (Summa Theol., I. liii) makes nomen connotans the equivalent of appellatio relativa, and takes the relation itself as the accusative object of connotare, speaking of ‘creator’ as connoting the relation of creator to creature. So Aquinas, In sentent., I. dist. viii. q. 1, Art. 1. Subsequently, because adjectives were looked upon as relative terms, white being defined as ‘having whiteness,’ &c., the adjective was looked upon as connoting the abstraction, but never unless its supposed relative character was under consideration. Tataretus, for example, who wrote when the usage was fully established, will be found using such phraseology as the following: ‘Nulla relativa secundum se habent contrarium, cum non sint qualitates primae, sed solum relativa secundum dici, et hoc secundum esse absolutum et significatum principale eorum et non secundum esse respectivum et connotativum.’ Chauvin (1st ed.) says: ‘Connotativum illud est cuius significatum non sistit in se, sed necessario ad aliud refertur, vel aliud connotat. V.g. Rex, magister, primus.’
It unfortunately happened, as the above quotations show, that the precise meaning recognized as proper to the word ‘signify’ at the time of John of Salisbury (a younger contemporary of Abelard) was never strictly observed, either before or since; and, on the contrary, the meaning tended to slip towards that of ‘denote.’ Yet even now the propriety of John's remark must be recognized.
A number of works were written in the middle ages De modis significandi, based upon Priscian (a contemporary of Boethius), who in turn followed Apollonius the bad-tempered, ‘grammaticorum princeps,’ who lived in the time of Hadrian and Antoninus Pius. Cf. also Thurot, Notices et Extraits des MSS., xxii. Pt. II, and Duns Scotus, Works, Lyons ed., 1. (C.S.P.) [528-9, CP 2.431-4]
Singular [Lat. singulus, separate; translates Gr. καθ’ ἑκαστον] : Ger. (1) einzeln, (1, 2) individuell; Fr. (1) individuel, (1, 2) singulier; Ital. (1) singolo, (2) singolare. (1) Applicable, as a sign, to a single individual.
(2) In mathematics : a singular place upon a continuum is a place whose properties differ from those of all other places in the vicinity, so as to constitute in one aspect a discontinuity. (C.S.P.)
Singular or Individual (in logic). A term which, during a given discussion, is not to be treated of in separate parts is a singular or individual term.
Like many expressions in logic, the signification is not absolute, but relative to the discussion in hand. Thus ‘my palette’ may be, upon one occasion, an indivisible object, and upon another it may be thought of as the field for many different colours. The technical definition is this: A is singular or individual if for every term whatever, x, either no A is x or else no A is non-x; in other words, there is nothing, x, such that A can be partly x and partly non-x. A proposition containing a singular term is called a ‘singular proposition.’ (C.L.F.) [533]
Subject (in logic). (1) That of which something is asserted in the form of a proposition; its conventional symbol is S. (J.M.B.)
(2) That part of a proposition whose function it is to ‘indicate,’ or denote, what it is of which the proposition is a SIGN (q. v.), and which it signifies, or indirectly images, in the predicate.
[What follows presents a view of propositions, à propos of ‘subject,’ developed on the basis of the theory of ‘signs’; it may be compared with the more commonly received view given under PROPOSITION. (J.M.B.)]
Whether or not every proposition has a principal subject, and, if so, whether it can or cannot have more than one, will be considered below. A proposition may be defined as a sign which separately indicates its object. For example, a portrait with the proper name of the original written below it is a proposition asserting that so that original looked. If this broad definition of a proposition be accepted, a proposition need not be a symbol. Thus a weathercock ‘tells’ from which direction the wind blows by virtue of a real relation which it would still have to the wind, even if it were never intended or understood to indicate the wind. It separately indicates the wind because its construction is such that it must point to the quarter from which the wind blows; and this construction is distinct from its position at any particular time. But what we usually mean by a proposition or judgment is a symbolic proposition, or symbol, separately indicating its object. Every subject partakes of the nature of an index, in that its function is the characteristic function of an index, that of forcing the attention upon its object. Yet the subject of a symbolic proposition cannot strictly be an index. When a baby points at a flower and says, ‘Pretty,’ that is a symbolic proposition; for the word ‘pretty’ being used, it represents its object only by virtue of a relation to it which it could not have if it were not intended and understood as a sign. The pointing arm, however, which is the subject of this proposition, usually indicates its object only by virtue of a relation to this object, which would still exist, though it were not intended or understood as a sign. But when it enters into the proposition as its subject, it indicates its object in another way. For it cannot be the subject of that symbolic proposition unless it is intended and understood to be so. Its merely being an index of the flower is not enough. It only becomes the subject of the proposition, because its being an index of the flower is evidence that it was intended to be. In like manner, all ordinary propositions refer to the real universe, and usually to the nearer environment. Thus, if somebody rushes into the room and says, ‘There is a great fire!’ we know he is talking about the neighbourhood and not about the world of the Arabian Nights' Entertainments. It is the circumstances under which the proposition is uttered or written which indicate that environment as that which is referred to. But they do so not simply as index of the environment, but as evidence of an intentional relation of the speech to its object, which relation it could not have if it were not intended for a sign. The expressed subject of an ordinary proposition approaches most nearly to the nature of an index when it is a proper name which, although its connection with its object is purely intentional, yet has no reason (or, at least, none is thought of in using it) except the mere desirability of giving the familiar object a designation. Among, or along with, proper names we may put abstractions, which are the names of fictitious individual things, or, more accurately, of individuals whose being consists in the manner of being of something else. A kind of abstractions are individual collections, such as the ‘German people.’ When the subject is not a proper name, or other designation of an individual within the experience (proximate or remote) of both speaker and auditor, the place of such designation is taken by a virtual precept stating how the hearer is to proceed in order to find an object to which the proposition is intended to refer. If this process does not involve a regular course of experimentation, all cases may be reduced to two with their complications. These are the two cases: first, that in which the auditor is to take any object of a given description, and it is left to him to take any one he likes; and, secondly, the case in which it is stated that a suitable object can be found within a certain range of experience, or among the existent individuals of a certain class. The former gives the distributed subject of a universal proposition, as, ‘Any cockatrice lays eggs.’ It is not asserted that any cockatrice exists, but only that, if the hearer can find a cockatrice, to that it is intended that the predicate shall be applicable. The other case gives the undistributed subject of a particular proposition, as ‘Some negro albino is handsome.’ This implies that there is at least one negro albino. Among complications of these cases we may reckon such subjects as that of the proposition, ‘Every fixed star but one is too distant to show a true disk,’ and, ‘There are at least two points common to all the circles osculating any given curve.’ The subject of a universal proposition may be taken to be, ‘Whatever object in the universe be taken’; thus the proposition about the cockatrice might be expressed: ‘Any object in the universe having been taken, it will either not be a cockatrice or it will lay eggs.’ So understood, the subject is not asserted to exist, but it is well known to exist; for the universe must be understood to be familiar to the speaker and hearer, or no communication about it would take place between them; for the universe is only known by experience. The particular proposition may still more naturally be expressed in this way, ‘There is something in the universe which is a negro albino that is handsome.’ No doubt there are grammatical differences between these ways of stating the fact; but formal logic does not undertake to provide for more than one way of expressing the same fact, unless a second way is requisite for the expression of inferences. The latter mode is, on the whole, preferable. A proposition may have several subjects. Thus the universe of projective geometry being understood, it is a true proposition that ‘Whatever individuals, A, B, C, and D may be, there are individuals E and F, such that whatever individual G may be, there is an individual H, and an individual I, such that, if A, B, C, and D are all straight lines, then E and F are straight lines, each intersecting A, B, C, and D, and E and F are not coincident; and if G is a straight line, not coincident with E, and not coincident with F, and if G intersects A, B, and C, it does not intersect D, unless H is a one-sheeted hyperboloid of which A, B, C, and D are generators, and J is a set of generators of H, to which A, B, C, and D all belong’; or, in our usual phraseology, any four straight lines in space are intersected by just two different straight lines, unless these four straight lines belong to one set of generators of a one-sheeted hyperboloid. Such a proposition is called a relative proposition. The order in which the selection of individuals is made is material when the selections are different in respect to distribution. The proposition may relate to the frequency with which, in the course of ordinary experience, a generic event is of a certain species. De Morgan wishes to erect this into the general type of propositions. But this is to overlook a vital distinction between probability and that which a universal proposition asserts. To say that the probability that a calf will not have more than six legs is 1, is to say that in the long run, taking calves as they present themselves in experience, the ratio of the number of those with not more than six legs to the total number is 1. But this does not prevent there being any finite number of calves with more legs than six, provided that in the long run, that is, in an endless course of experience, their number remains finite, and does not increase indefinitely. A universal proposition, on the other hand, asserts, for example, that any calf which may exist, without exception, is a vertebrate animal. The universal proposition speaks of experience distributively; the probable, or statistical proposition, speaks of experience collectively. (C.S.P.) [608-10, CP 2.357]
Symbol [Gr. συμβολον, a conventional sign, from συν + βαλλειν, to throw]: Ger. Symbol; Fr. symbole; Ital. simbolo. (1) A SIGN (q.v.) which is constituted a sign merely or mainly by the fact that it is used and understood as such, whether the habit is natural or conventional, and without regard to the motives which originally governed its selection.
Συμβολον is used in this sense by Aristotle several times in the Peri hermeneias, in the Sophistici Elenchi, and elsewhere.
(2) An algebraic character. (C.S.P.) [640]
Synechism [Gr. συνεχής, continuous, holding together, from σύν + ἔχειν, to hold] : not in use in the other languages. That tendency of philosophical thought which insists upon the idea of continuity as of prime importance in philosophy, and in particular, upon the necessity of hypotheses involving true continuity.
A true CONTINUUM (q. v.) is something whose possibilities of determination no multitude of individuals can exhaust. Thus, no collection of points placed upon a truly continuous line can fill the line so as to leave no room for others, although that collection had a point for every value towards which numbers endlessly continued into the decimal places could approximate; nor if it contained a point for every possible permutation of all such values. It would be in the general spirit of synechism to hold that time ought to be supposed truly continuous in that sense. The term was suggested and used by C. S. Peirce in the Monist, ii. 534 (July, 1892). Cf. PRAGMATISM, passim.
The general motive is to avoid the hypothesis that this or that is inexplicable. For the synechist maintains that the only possible justification for so much as entertaining a hypothesis, is that it affords an explanation of the phenomena. Now, to suppose a thing inexplicable is not only to fail to explain it, and so to make an unjustifiable hypothesis, but much worse—it is to set up a barrier across the road of science, and to forbid all attempt to understand the phenomenon.
To be sure, the synechist cannot deny that there is an element of the inexplicable and ultimate, because it is directly forced upon him; nor does he abstain from generalizing from this experience. True generality is, in fact, nothing but a rudimentary form of true continuity. Continuity is nothing but perfect generality of a law of relationship.
It would, therefore, be most contrary to his own principle for the synechist not to generalize from that which experience forces upon him, especially since it is only so far as facts can be generalized that they can be understood; and the very reality, in his way of looking at the matter, is nothing else than the way in which facts must ultimately come to be understood. There would be a contradiction here, if this ultimacy were looked upon as something to be absolutely realized; but the synechist cannot consistently so regard it. Synechism is not an ultimate and absolute metaphysical doctrine; it is a regulative principle of logic, prescribing what sort of hypotheses are lit to be entertained and examined. The synechist, for example, would never be satisfied with the hypothesis that matter is composed of atoms, all spherical and exactly alike. If this is the only hypothesis that the mathematicians are as yet in condition to handle, it may be supposed that it may have features of resemblance with the truth. But neither the eternity of the atoms nor their precise resemblance is, in the synechist's view, an element of the hypothesis that is even admissible hypothetically. For that would be to attempt to explain the phenomena by means of an absolute inexplicability. In like manner, it is not a hypothesis fit to be entertained that any given law is absolutely accurate. It is not, upon synechist principles, a question to be asked, whether the three angles of a triangle amount precisely to two right angles, but only whether the sum is greater or less. So the synechist will not believe that some things are conscious and some unconscious, unless by consciousness be meant a certain grade of feeling. He will rather ask what are the circumstances which raise this grade; nor will he consider that a chemical formula for protoplasm would be a sufficient answer. In short, synechism amounts to the principle that inexplicabilities are not to be considered as possible explanations; that whatever is supposed to be ultimate is supposed to be inexplicable; that continuity is the absence of ultimate parts in that which is divisible; and that the form under which alone anything can be understood is the form of generality, which is the same thing as continuity. (C.S.P.) [657, CP 6.169-73]
Synthetic (-al) : Ger. synthetisch; Fr. synthétique; Ital. sintetico. Having or producing the unity of a SYNTHESIS (q. v.).
Synthetic(-al) argument, inference, reasoning, &c. An argument whose conclusion expresses a fact the being of which is given in the being of the premises, so that the conclusion could not be false as long as the premise is true, is analytical; any other mode of argument is synthetical.
A synthetical argument may be a fallacy. In that case, it may be so absurd as not to be an argument in any other sense than that it professes to be so. But if it is an argument (as commonly happens) the real argument is either inductive or presumptive in its nature, these being the two types of synthetic argumentation.
Synthetic judgment: see ANALYTIC AND SYNTHETIC JUDGMENT, KANT S TERMINOLOGY (Glossary, ‘synthetische Urtheile’), HEGEL'S TERMINOLOGY (Dialectic, III, IV), SYNTHETIC PHILOSOPHY, and SYNTHESIS (different topics).
Synthetic method (in logic). What is commonly, very confusedly, meant by a synthetic method is a progressive deductive method, more or less of the nature of reasoning in Barbara.
The confusion between analysis and synthesis is so great (cf. ANALYTIC AND SYNTHETIC JUDGMENT), and the distinction is founded upon such false views of logic, that it is perhaps best to abandon the words altogether in logic. (C.S.P.) [658-9]
Term [Lat. terminus, trans. of Gr. ὁρος, literally a boundary; there is a Greek word τερμα, but it is not used in a logical sense]: Ger. Terminus; Fr. terme; Ital. termine. (1) One of the principal parts of a PROPOSITION (q. v.). If from the proposition ‘Socrates is mortal’ we strike out the separate indication of the subject we have ‘______ is mortal’; and this ought to be regarded as a term. It is usually stated that ‘mortal’ is the term; but if there is any difference, it should rather be ‘_____ is mortal.’
In most languages no separate word ‘is’ is required to assert that ‘Socrates is mortal’ and as long as Greek was the language of logic, in which an is may lie inserted or may be omitted, little importance was attached to the is. But the Latin logicians of the 12th century began to regard this as essential, and thus made a distinction between ‘is mortal’ and ‘mortal,’ which relates to the peculiarities of a small class of languages. Thereafter logicians, and especially nominalists, began to regard terms no longer as parts of propositions, but as general names having an existence and meaning irrespective of any potential proposition. In most languages there appear not to be any such nouns, or very few. In Semitic languages, for example, common nouns are thought as parts of verbs, approaching the nature of participles, as most of them in fact are. It is, therefore, scarcely more true that they are mere names than that our words ‘seeing’ and ‘dying’ or ‘moriturus’ are names. There is in connection with them the idea of their being fragments of possible propositions; and so much so, that the mere adjunction of two of them makes a proposition.
If, however, we are to take term as meaning a word used as the sign of (to designate) an independent individual object, then it is proper to notice that there are many other signs of that nature. We may therefore generalize the meaning of ‘term,’ and define it (in the general sense) as a sign which does not separately indicate its object, and therefore cannot separately determine its interpretant.
The ordinary logics overlook relative terms. ‘Anything whatever is mother only of things loved by itself’ is a proposition beyond dispute, since it is true or false. Therefore it must have a predicate: this is, ‘is mother only of things loved by’; or it may be taken to be, ‘is mothered only by lovers of’; or, ‘loves everything mothered by’; or, ‘is either lover of or not mother of’; &c. Relative terms once admitted, it becomes evident that every verb is a term, the difference between ‘loves’ and ‘lover’ being merely that the rules of grammar prescribe different syntax for them. On the other hand, there are various words used in propositions which are not terms, because they cannot take the place of proper names. ‘Any’ may be considered as meaning ‘Whatever is,’ or ‘The individual which the reader selects,’ and so as a term; and in like manner ‘Some’ may be taken as meaning ‘The object the wise friend of the speaker selects,’ or something of the sort. Relative pronouns, however, together with the letters A,B,C, &c., often used as relative pronouns of an improved kind, if symbols at all, are so extremely like indices that they may for ordinary purposes be so considered.
Abstract terms are matters of extreme importance in all difficult reasoning. Thus, in geometry, we define a point as a completely determinate place, an instant as a completely determinate time, and a particle as that which in any instant is at one point and not at any other. But in a time not completely determined a particle moves. We express that by abstract term line as the place in which a particle may be in the course of time. The advantage of doing this is that it enables us to consider relations of lines and their motions, which we could not have done without the abstraction.
(2) A relation is said to have terms, which are the objects thus related the one to another. So we speak of the terms of a ratio or proportion.
Absolute term: a term like a common substantive word which connotes nothing.
Ampliate and ampliative terms. An ampliative term is a term which when in the predicate causes its subject, the ampliate term, to denote more than before. Among ampliative terms are reckoned by Scotus (in I Priorum, qu. xvi) verbs in future and past tenses, and future and preterite participles; also such verbs as potest, contingit, and names derived from them; also significo, intelligo, promitto, and the like, and in general every verb whose object may be indifferently a present or future thing.
Concrete term: a term not abstract, whether it be a substantive or purely denotative term (according to the mediaeval doctrine) or an appellative or connotative term.
Connotative term: a term which, in addition to ‘supponere pro,’ or directly denoting something, also connotes that that principally denoted thing has some essential or accidental aspect. Such is ‘white,’ which means ‘having whiteness.’
Denominative term: a NAME (q. v.).
[Designate term (and designation): a term which is used to indicate merely a particular object or class of objects; the application of such a term is ‘designation.’—J.M.B.]
Discrete term: a term which denotes one sole individual, but this may be an individual collection, or system.
Exponible term: a syncategorematic word making a proposition exponible, that is, exceptive, exclusive, reduplicative, inceptive, comparative, &c. (C.S.P.) [675-7; followed by C.L.F. definition of Negative term.]
Testimony [Lat. testimonium, from testis, a witness]: Ger. Zeugniss; Fr. témoignage; Ital. testimonianza. The statement of a witness used as evidence, whether depositional or documentary.
Deposition is oral or written. All testimony is either direct or circumstantial. Direct testimony is a statement of the very fact in question. Testimony is, further, either intentional or casual. Intentional testimony is a statement made for the purpose of persuading those before whom it is laid of the truth of the facts in question. Testimony is further either original or second-hand. Original testimony is testimony to percepts, or perceptual judgments, of the witness. Second-hand testimony is testimony as to what the witness learned by testimony (strictly by original testimony, otherwise it would be third-hand, &c., testimony, or rumour).
There is a general tendency to believe what one is told; and, as in the case of other such tendencies, it should at first be followed, although cautiously and tentatively. Even when experience is wanting, as for example in examining a prisoner, although greater caution is required, the proper course is to begin with the presumption that the testimony is true, for unless we make such a presumption, no truth can ever be discovered. It is true that the unlikelihood of the matter of the testimony may cause immediate distrust, or even disbelief of it, but no persons are so frequently deceived as those who stop to weigh likelihoods before accepting or rejecting testimony, and who then form a confident opinion pro or con. Testimony should almost always be accepted as approximately correct, but always strictly on probation, as a subject of examination. In our legal proceedings, witnesses are subject to cross-examination. Everybody is agreed that this is an essential step in the inquiry, but in a historical inquiry no such thing is possible. Still the testimony can be tested in various ways; and this must be done. But in any case, the rendering of the testimony is a fact which needs to be accounted for; and by whatever theory it be proposed to account for it, that theory needs to be checked and tested. Properly handled, false testimony may often yield a great deal of information.
An experimental test may be readily performed by considering the least antecedently likely but necessary or highly probable consequence of the theory, which is susceptible of being confronted with observation direct or indirect. If this consequence is found, notwithstanding its unlikelihood, to be true, there is then some reason for believing in the theory proposed to account for the testimony. (C.S.P.-J.M.B.) [686]
Thema [Gr. θεμα, a deposit, dépôt, stakes, theme]: Ger. Thema; Fr. thème; Ital. tema. A word proposed in 1635 by Burgersdicius in his Logic (I. ii. § 1), for that ‘quod intellectui cognoscendum proponi potest’; but what he seems to mean is what Aristotle sometimes vaguely expresses by λογος, the immediate object of a thought, a meaning.
It is of the nature of a sign, and in particular of a sign which is rendered significant by a character which lies in the fact that it will be interpreted as a sign. Of course, nothing is a sign unless it is interpreted as a sign; but the character which causes it to be interpreted as referring to its object may be one which might belong to it irrespective of its object and though that object had never existed, or it may be in a relation to its object which it would have just the same whether it were interpreted as a sign or not. But the thema of Burgersdicius seems to be a sign which, like a word, is connected with its object by a convention that it shall be so understood, or else by a natural instinct or intellectual act which takes it as a representative of its object without any action necessarily taking place which should establish a factual connection between sign and object. If this was the meaning of Burgersdicius, his thema is the same as the present writer's ‘symbol’ (see SIGN). (C.S.P.) [691-2, CP 2.308]
Theorem [Gr. θεωρημα]: Ger. Theorem, Lehrsatz; Fr. théorème; Ital. teorema. A demonstrable theoretical proposition. (C.S.P.) [693]
Theory (in science): [Gr. θεωρία, a contemplation, speculation]: Ger. Theorie; Fr. théorie; Ital. teoria. A general principle or formula propounded for the purpose of explaining phenomena, as the ‘theory of gravitation,’ or the Newtonian theory.
In modern nomenclature it is confined to principles the truth of which has at least a large measurement of plausibility, in contradistinction to a hypothesis, which is propounded as a tentative explanation, the truth of which is to be verified or disproved by subsequent research. (S.N.)
The whole aim of science is to find out facts, and to work out a satisfactory theory of them. Still, a theory does not necessarily lose its utility by not being altogether true. It must be intelligible and diagrammatical, or it has no title to the name theory. The facts to which it refers are not necessarily facts of experience; they may be relations of pure mathematical forms. A theory is properly a result of systematic scientific consideration, not of mere casual suggestions; and thus the word bears a somewhat eulogistic implication in contrast to ‘view.’ Theory is opposed to fact; the latter meaning, in this connection, that which is forced upon us by perception; while theory is the part of science which is contributed by the intellect and confirmed by experiment. Theory is also opposed to practice; because a theory is a scientific product, and a pure, or theoretical, theory has regard to science alone, and is often in conflict with the practical theory, which ought preferably to be the guide of immediate action. But the latter is as truly a theory as the former, and ought equally (when practicable) to be a product of scientific examination. That which science recommends for its own use in a secular investigation may be different from what it prescribes as a basis for instant action.
Every theory has its beginning in hypothesis. For, except perhaps in pure mathematics, the presumptive adoption of a hypothesis is the only possible way of framing a judgment concerning things beyond perception; unless we consider instinctive judgments as an exception. Neither is the situation essentially otherwise in pure mathematics. A mathematical theory supposes a broad conception of the forms to which it relates. This is known to be true of them only by a process of demonstration, which in many cases has to wait for several years for its accomplishment, and in all cases must be subsequent to the first beginnings of the theory. It may be that a quasi-induction has created a belief in a mathematical theorem before it has been demonstrated. But a valid and genuine induction is not possible in pure mathematics, for the reason that genuine induction essentially relates to the ratio of frequency of a specific phenomenon to a generic phenomenon in the ordinary course of experience. Now in pure mathematics, which deals with figments of our own creation, there is nothing at all to correspond accurately to a course of experience. Suppose we find, for example, that in a complicated development there is a certain regular relation among the first terms. If there is no obscure demonstrative insight which assures us that this must be, it is quite possible that, as the series goes on, a state of things may intervene which interferes with that relation, and if so, the proportion of terms that will accord with that formula will presumably be very far from 1:1. There is, therefore, no security of the nature which belongs to induction, that as the instances are multiplied the observed ratio will indefinitely approximate to the true ratio. This sort of induction, therefore, has no other validity than such as belongs to a hypothesis which suits the facts as far as we yet know them. If it is to be called an induction, it is a degenerate induction differing very little from hypothesis. It may properly be said, then, that even a pure mathematical theory is developed out of hypotheses.
No theory in the positive sciences can be supposed to satisfy every feature of the facts. Although we know that the law of gravitation is one of the most perfect of theories, yet still, if bodies were to attract one another inversely as a power of the distance whose exponent were not 2, but 2.000001, the only observable effect would be a very slow rotation of the line of apsides of each planet. Now the lines of apsides all do rotate in consequence of perturbations, which virtually do alter slightly the sun's attraction, and thus such an effect would probably only produce slight discrepancies in the values obtained for the masses of the planets. In very many cases, especially in practical problems, we deliberately go upon theories which we know are not exactly true, but which have the advantage of a simplicity which enables us to deduce their consequences. This is true of almost every theory used by engineers of all kinds. The most extraordinary departure from the known facts occurs when hydrodynamics is applied, where the theory is in striking opposition to facts which obtrude themselves upon every spectator of moving water. Nevertheless, even in this case, the theory is not useless.
In all the explanatory sciences theories far more simple than the real facts are of the utmost service in enabling us to analyze the phenomena, and it may truly be said that physics could not possibly deal even with its relatively simple facts without such analytic procedure. Thus, the kinetical theory of gases, when first propounded, was obliged to assume that all the molecules were elastic spheres which nobody could believe to be true. If this is necessary even in physics, it is far more indispensable in every other science, and most of all in the moral sciences, such as political economy. Here the sane method is to begin by considering persons placed in situations of extreme simplicity, in the utmost contrast to those of all human society, as animated by motives and by reasoning power equally unlike those of real men. Nevertheless, in this way alone can a base be obtained from which to proceed to the consideration of the effects of different complications. Owing to the necessity of making theories far more simple than the real facts, we are obliged to be cautious in accepting the consequences of them, and to be also upon our guard against apparent refutations of them based upon such extreme consequences.
Whewell makes a great point of the relativity of the distinction between theory and fact. This is an important point that ought not to be overlooked. Every fact involves an element supplied by the mind, which if not, properly speaking, theory, is analogous to theory. On the other hand, serious errors of logic will result from not taking account of the difference between the intellectual elements already involved in the perceptual acts and scientific theories. A theory is a result subject to criticism, meaning by criticism, not the consideration of whether or how far an object is beautiful, useful, or the like, but the passing of a judgment as to whether the object ought to be as it is or as it is proposed to make it. If this judgment is adverse, the theory can and will be altered; and it will not be maintained by anybody until it is put into a shape to withstand his criticism. But it is perfectly idle, in this sense of the word, for anybody to criticize what he cannot help, and, like other idle and unamiable practices, it is also highly pernicious. Now all the subconscious work of the intellect in framing a percept and a perceptual judgment is beyond our control, and therefore not subject to logical criticism. It simply has to be accepted. Kant, perhaps, did not sufficiently appreciate this when he undertook to study the critic of such mental forms as space, time, unity, reality, &c.; but, after all, his deduction of the categories is merely in outcome that knowledge cannot be had on other terms; that is, that they are inevitable. Perceptual judgments, therefore, are, for the purposes of logical criticism, absolute facts without any admixture of theory. If a theory does not square with perceptual facts it must be changed. But the impressions of sense from which it is supposed that the percepts have been constructed are matters of theory. If the percepts were proved not to square with the impressions of sense, it would not at all be the percepts that would have to be reformed, for they cannot be reformed; it would be, on the contrary, that theory, that the percepts are constructed out of impressions of sense that would have to be modified. (C.S.P., C.L.F.) [693-4; CP 7.94-6]
Thesis [Gr. θεσις, a placing or setting; also, in the modern sense, and apparently sometimes to mean merely a universal proposition]: Ger. These; Fr. thèse; Ital. tesi. An assertion formally stated preparatory to a regular defence of it by argumentation.
The Latin form position is less formal in its implication. The denial of a thesis preparatory to regular counter-argumentation is sometimes called the antithesis; but this is rarely used except with reference to Kant's antinomies. In geometry, the abstract statement of a theorem is called the enunciation, or first enunciation; the statement with reference to the diagram being called the second enunciation, or statement. The latter is also called the ecthesis, or exposition. For other meanings of thesis, see The Century Dictionary. (C.S.P.), C.L.F.) [695]
Transposition (in logic) [Lat. trans + ponere, to place]: Ger. Hinüberschaffen; Fr. transposition; Ital. trazposizione. Transposition consists in transferring a term from the subject to the predicate, or the reverse, with no change in the character of the connection; as, No artists who are bankers are clever, No artists are clever bankers, No bankers are clever artists, None are at once artists and bankers and clever; or as All but a is b, All but b is a. Any proposition may be ‘transformed’ into other exactly equivalent forms: e.g. the transformation may consist in the change from one sort of connection to another (change of copula, in the extended meaning of that term), as – to take a compound proposition as an example – It never rains but it pours = always either it pours or it does not rain, but this is not transposition.
Certain copulas permit transposition simply, with no variation in the quality of the term transposed (as in the instances just given); but with the non-symmetrical copulas (see PROPOSITION) there must be a change from positive to negative or the reverse (and, if the proposition is complex, from the conjunctive to the alternative combination and the reverse), if the change can be made at all: He who is an astronomer and un-devout is mad = Any astronomer is mad or devout = All are mad or devout or not astronomers. When both the whole subject and the whole predicate is transposed the change is commonly called contraposition if the copula is non-symmetrical (All a is b = All non-b is non-a; None but a is b = None but non-b is non-a), but simple conversion if it is symmetrical (No a is b = No b is a, Some a is b = Some b is a). The usual discussion in the logics of the doctrine of the equivalence of propositions is greatly simplified by taking this more general view of the subject (see PROPOSITION). (C.S.P., C.L.F.) [713; CP 3.644-5]
Truth (and Falsity and Error)
…
Logical. (1) Truth is a character which attaches to an abstract proposition, such as a person might utter. It essentially depends upon that proposition's not professing to be exactly true. But we hope that in the progress of science its error will indefinitely diminish, just as the error of 3.14159, the value given for π, will indefinitely diminish as the calculation is carried to more and more places of decimals. What we call π is an ideal limit to which no numerical expression can be perfectly true. If our hope is vain; if in respect to some question—say that of the freedom of the will—no matter how long the discussion goes on, no matter how scientific our methods may become, there never will be a time when we can fully satisfy ourselves either that the question has no meaning, or that one answer or the other explains the facts, then in regard to that question there certainly is no truth. But whether or not there would be perhaps any reality is a question for the metaphysician, not the logician. Even if the metaphysician decides that where there is no truth there is no reality, still the distinction between the character of truth and the character of reality is plain and definable. Truth is that concordance of an abstract statement with the ideal limit towards which endless investigation would tend to bring scientific belief, which concordance the abstract statement may possess by virtue of the confession of its inaccuracy and one-sidedness, and this confession is an essential ingredient of truth. A further explanation of what this concordance consists in will be given below. Reality is that mode of being by virtue of which the real thing is as it is, irrespectively of what any mind or any definite collection of minds may represent it to be. The truth of the proposition that Caesar crossed the Rubicon consists in the fact that the further we push our archaeological and other studies, the more strongly will that conclusion force itself on our minds forever—or would do so, if study were to go on forever. An idealist metaphysician may hold that therein also lies the whole reality behind the proposition; for though men may for a time persuade themselves that Caesar did not cross the Rubicon, and may contrive to render this belief universal for any number of generations, yet ultimately research—if it be persisted in—must bring back the contrary belief. But in holding that doctrine, the idealist necessarily draws the distinction between truth and reality. [Cf., however, the section Psychological, below. — J.M.B.]
In the above we have considered positive scientific truth. But the same definitions equally hold in the normative sciences. If a moralist describes an ideal as the summum bonum, in the first place, the perfect truth of his statement requires that it should involve the confession that the perfect doctrine can neither be stated nor conceived. If, with that allowance, the future development of man's moral nature will only lead to a firmer satisfaction with the described ideal, the doctrine is true. A metaphysician may hold that the fact that the ideal thus forces itself upon the mind, so that minds in their development cannot fail to come to accept it, argues that the ideal is real: he may even hold that that fact (if it be one) constitutes a reality. But the two ideas, truth and reality, are distinguished here by the same characters given in the above definitions.
These characters equally apply to pure mathematics. Projective geometry is not pure mathematics, unless it be recognized that whatever is said of rays holds good of every family of curves of which there is one and one only through any two points, and any two of which have a point in common. But even then it is not pure mathematics until for points we put any complete determinations of any two-dimensional continuum. Nor will that be enough. A proposition is not a statement of perfectly pure mathematics until it is devoid of all definite meaning, and comes to this—that a property of a certain icon is pointed out and is declared to belong to anything like it, of which instances are given. The perfect truth cannot be stated, except in the sense that it confesses its imperfection. The pure mathematician deals exclusively with hypotheses. Whether or not there is any corresponding real thing, he does not care. His hypotheses are creatures of his own imagination; but he discovers in them relations which surprise him sometimes. A metaphysician may hold that this very forcing upon the mathematician's acceptance of propositions for which he was not prepared, proves, or even constitutes, a mode of being independent of the mathematician's thought, and so a reality. But whether there is any reality or not, the truth of the pure mathematical proposition is constituted by the impossibility of ever finding a case in which it fails. This, however, is only possible if we confess the impossibility of precisely defining it.
The same definitions hold for the propositions of practical life. A man buys a bay horse, under a warranty that he is sound and free from vice. He brings him home and finds he is dyed, his real colour being undesirable. He complains of false representations; but the seller replies, ‘I never pretended to state every fact about the horse; what I said was true, so far as it professed to be true.’ In ordinary life all our statements, it is well understood, are, in the main, rough approximations to what we mean to convey. A tone or gesture is often the most definite part of what is said. Even with regard to perceptual facts, or the immediate judgments we make concerning our single percepts, the same distinction is plain. The percept is the reality. It is not in propositional form. But the most immediate judgment concerning it is abstract. It is therefore essentially unlike the reality, although it must be accepted as true to that reality. Its truth consists in the fact that it is impossible to correct it, and in the fact that it only professes to consider one aspect of the percept.
But even if it were impossible to distinguish between truth and reality, that would not in the least prevent our defining what it is that truth consists in. Truth and falsity are characters confined to propositions. A proposition is a sign which separately indicates its object. Thus, a portrait with the name of the original below it is a proposition. It asserts that if anybody looks at it, he can form a reasonably correct idea of how the original looked. A sign is only a sign in actu by virtue of its receiving an interpretation, that is, by virtue of its determining another sign of the same object. This is as true of mental judgments as it is of external signs. To say that a proposition is true is to say that every interpretation of it is true. Two propositions are equivalent when either might have been an interpretant of the other. This equivalence, like others, is by an act of abstraction (in the sense in which forming an abstract noun is abstraction) conceived as identity. And we speak of believing in a proposition, having in mind an entire collection of equivalent propositions with their partial interpretants. Thus, two persons are said to have the same proposition in mind. The interpretant of a proposition is itself a proposition. Any necessary inference from a proposition is an interpretant of it. When we speak of truth and falsity, we refer to the possibility of the proposition being refuted; and this refutation (roughly speaking) takes place in but one way. Namely, an interpretant of the proposition would, if believed, produce the expectation of a certain description of percept on a certain occasion. The occasion arrives: the percept forced upon us is different. This constitutes the falsity of every proposition of which the disappointing prediction was the interpretant.
Thus, a false proposition is a proposition of which some interpretant represents that, on an occasion which it indicates, a percept will have a certain character, while the immediate perceptual judgment on that occasion is that the percept has not that character. A true proposition is a proposition belief in which would never lead to such disappointment so long as the proposition is not understood otherwise than it was intended.
All the above relates to complex truth, or the truth of propositions. This is divided into many varieties, among which may be mentioned ethical truth, or the conformity of an assertion to the speaker's or writer's belief, otherwise called veracity, and logical truth, that is, the concordance of a proposition with reality, in such way as is above defined.
(2) The word truth has also had great importance in philosophy in widely different senses, in which it is distinguished as simple truth, which is that truth which inheres in other subjects than propositions.
Plato in the Cratylus (385 B) maintains that words have truth; and some of the scholastics admitted that an incomplex sign, such as a picture, may have truth.
But truth is also used in senses in which it is not an affection of a sign, but of things as things. Such truth is called transcendental truth. The scholastic maxim was Ens est unum, verum, bonum. Among the senses in which transcendental truth was spoken of was that in which it was said that all science has for its object the investigation of truth, that is to say, of the real characters of things. It was, in other senses, regarded as a subject of metaphysics exclusively. It is sometimes defined so as to be indistinguishable from reality, or real existence. Another common definition is that truth is the conformity, or conformability, of things to reason. Another definition is that truth is the conformity of things to their essential principles.
(3) Truth is also used in logic in a sense in which it inheres only in subjects more complex than propositions. Such is formal truth, which belongs to an argumentation which conforms to logical laws. (C.S.P.) [718-20, followed by Psychological (J.M.B., C.L.F.); CP 5.565-73]
Ultimate [Lat. ultimus, furthest]: Ger. allerletzt, End-(glied, &c.); Fr. dernier, ultime, final; Ital. ultimo. (1) Last in a series; especially, in a series of purposes each, except the last, subsidiary to an ulterior one following it in the arrangement considered, or of actions each of which, except the last, leads to the performance of another.
Thus, the phrase ultimate signification implies that a sign determines another sign of the same object, and this another; and so on until something is reached which is a sign only for itself. Ultimate fact implies that there is a series of facts each explicable by the one following it, until a fact is reached utterly inexplicable. (Cf. Hamilton's Reid, Note A, § 5, II vi. et seq.).
(2) Applied also to the limiting state of an endless series of states which approach indefinitely near to the limiting state, and on the whole nearer and nearer, without necessarily ever reaching it; although the word ultimate does not imply a denial of actual attainment.
Thus, it has been held that a real object is that which will be represented in the ultimate opinion about it. This implies that a series of opinions succeed one another, and that it is hoped that they may ultimately tend more and more towards some limiting opinion, even if they do not reach and rest in a last opinion. Cf. TRUTH AND ERROR, Logical. (C.S.P.) [723-4]
Uniformity [Lat. unus, one, + forma, shape: Ger. Ein- (or Gleich-) förmigkeit; Fr. uniformité; Ital. uniformità. (1) A fact consisting in this: that, of a certain genus of facts, a proportion approaching unity (the whole) belongs, in the course of experience, to a certain species; so that, though of itself the knowledge of this uniformity gives no information concerning a certain thing or character, yet it will strengthen any inductive conclusion of a certain kind.
It is, therefore, a high objective probability concerning an objective probability. There are, in particular, four classes of uniformities, the knowledge of any of which, or of its falsity, may deductively strengthen or weaken an inductive conclusion. These four kinds of uniformity are as follows:—
i. The members of a class may present an extraordinary resemblance to one another in regard to a certain line of characters. Thus, the Icelanders are said to resemble one another most strikingly in their opinions about general subjects. Knowing this, we should not need to question many Icelanders, if we found that the first few whom we met all shared a common superstition, in order to conclude with considerable confidence that nearly all Icelanders were of the same way of thinking. Philodemus insists strongly upon this kind of uniformity as a support of induction.
ii. A character may be such that, in whatever genus it occurs at all, it almost always belongs to all the species of that genus; or this uniformity may be lacking. Thus, when only white swans were known, it would have been hazardous to assert that all swans were white, because whiteness is not usually a generic character. It is considerably more safe to assert that all crows are black, because blackness is oftener a generic character. This kind of uniformity is especially emphasized by J. S. Mill as important in inductive inquiries.
iii. A certain set of characters may be intimately connected so as to be usually all present or all absent from certain kinds of objects. Thus, the different chemical reactions of gold are so inseparable that a chemist need only to succeed in getting, say, the purple of Cassius to be confident that the body under examination will show every reaction of gold.
iv. Of a certain object it may be known that its characteristic is that when it possesses one of a set of characters within a certain group of such sets, it possesses the rest. Thus, it may be known of a certain man that to whatever party he belongs, he is apt to embrace without reserve the entire creed of that party. We shall not, then, need to know many of his opinions, say in regard to politics, in order to infer with great confidence his position upon other political questions.
(2) The word ‘uniformity’ plays such a singular and prominent rôle in the logic of J. S. Mill that it is proper to note it. He was apt to be greatly influenced by Ockham's razor in forming theories which he defended with great logical acumen; but he differed from other men of that way of thinking in that his natural candour led to his making many admissions without perceiving how fatal they were to his negative theories. In addition to that, perhaps more than other philosophers, in endeavouring to embrace several ideas under a common term, he often leaves us at a loss to find any other character common and peculiar to those notions except that of their having received from him that common designation. In one passage of his System of Logic (1842), he declares, in reference to the difference in strength between two inductive conclusions, that whoever shall discover the cause of that difference will have discovered the secret of inductive reasoning. When, therefore, he shortly afterwards points out that the distinction between those two inductions is that one of them is supported by a uniformity of the second of the above four classes, while the other is met by a distinct diversity of the same kind, and when he himself gives to that uniformity this designation when he afterwards declares that the validity of induction depends upon uniformity, his reader naturally supposes he means uniformity in that sense. But we find that he employs the word for quite another purpose. Namely, he does not like the word law, as applied to an inductive generalization of natural facts—such as the ‘law’ of gravitation—because it implies an element in nature, the reality of a general, which no nominalist can admit. He, therefore, desires to call the reality to which a true universal proposition about natural phenomena corresponds a ‘uniformity.’ The implication of the word, thus used, is that the facts are, in themselves, entirely disconnected, and that it is the mind alone which unites them. One stone dropping to the earth has no real connection with another stone dropping to the earth. It is, surely, not difficult to see that this theory of uniformities, far from helping to establish the validity of induction, would be, if consistently admitted, an insuperable objection to such validity. For if two facts, A and B, are entirely independent in their real nature, then the truth of B cannot follow, either necessarily or probably, from the truth of A. If I have tried the experiment with a million stones and have found that every one of them fell when allowed to drop, it may be very natural for me to believe that almost any stone will act in the same way. But if it can be proved that there is no real connection between the behaviour of different stones, then there is nothing for it but to say that it was a chance coincidence that those million stones all behaved in the same way; for if there was any reason for it, and they really dropped, there was a real reason, that is, a real general. Now, if it is mere chance that they all dropped, that affords no more reason for supposing that the next will drop than my throwing three double sixes successively with a pair of dice is a reason for thinking that the next throw will be double-sixes.
(3) But now we find that Mill's good sense and candour will not allow him to take the course which a Hobbes would have taken, and utterly deny the validity of induction; and this leads to a new use of the word uniformity, in which he speaks of the ‘uniformity of nature.’ Before asking exactly what this phrase means, it may be noted that, whatever it means, the assertion of it is an assent to scholastic realism, except for a difference of emphasis. For to say that throughout the whole course of experience, events always, or even only usually, happen alike under the same conditions (what is usually called the ‘invariability’ of nature) is to assert an agreement (complete or partial) which could not be ascribed to chance without self-contradiction. For chance is merely the possible discrepancy between the character of the limited experience to which it belongs and the whole course of experience. Hence, to say that of the real, objective facts some general character can be predicated, is to assert the reality of a general. It only differs from scholastic realism in that Mill and his followers treat this aspect of the matter lightly—that is to say, the objective reality of the general—while the Scholastics regarded it as a great and vital feature of the universe. Instead of ‘uniformity’ now importing that what others call ‘laws’ are fabrications of the human mind, this ‘uniformity of nature’ is erected by Mill into the greatest of laws and absolutely objective and real.
Let us now inquire what the ‘uniformity of nature,’ with its synonymous expressions that ‘the future resembles the past,’ and so forth, can mean. Mill says that it means that if all the circumstances attending two phenomena are the same, they will be alike. But taken strictly this means absolutely nothing, since no two phenomena ever can happen in circumstances precisely alike, nor are two phenomena precisely alike. It is, therefore, necessary to modify the statement in order to give it any meaning at all; and it will be found that, however it may be so modified, the moment it begins to carry a definite meaning, one of three things results: it becomes either, first, grossly false, or, second, an assertion which there is really no good reason to believe even approximately true, or, thirdly, it becomes a quasi-subjective truth, not lending any colour of validity to induction proper. If, for example, we were to say that, under any given species of circumstances presenting any similarity, phenomena of any given genus would be found to have a specific general resemblance in contrast with the specific character of phenomena of the same genus occurring under a different species of circumstances of the same genus, this would be monstrously false, whether intended as an absolutely universal proposition or merely as one approximately true. Let, for example, the genus of phenomena be the values of the throws of a pair of dice in a given series of successive throws indefinitely continued. Let the first species of circumstances be that the ordinal number of a throw in the series is prime. It is pretty certain that there would be no general character in the corresponding values of throws to distinguish them from those which would result when the ordinal number is divisible by 2, or by 3, or by any other prime. It thus appears that when we take any genus of circumstances, the law turns out false. Suppose, then, that we modify it by saying that, taking any genus of phenomena and separating this into two species, there will be found in the discoverable circumstances some general resemblance for all those attending phenomena of the same species in contrast to those attending phenomena of the other species. This is a proposition which there is not the slightest reason to believe. Take, for example, as the genus of phenomena, the many thousands of Latin descriptions of American species of plants by Asa Gray and his scholars. Now consider the species of this genus of phenomena which agree in this respect, that the two first words of the description have their first vowels the same. There is no reason to suppose that there was any general respect in which the circumstances of that species of the genus of phenomena agree with one another and differ from others, either universally or usually. It is a mere chance result. It is true that some persons will not be inclined to assent to this judgment; but they cannot prove it otherwise. It can afford no adequate basis for induction. We see, then, that when we consider all phenomena, there is no way of making the statement sufficiently definite and certain. Suppose, then, that we attempt still another modification of the law, that, of interesting resemblances and differences between phenomena, some considerable proportion are accompanied by corresponding resemblances and differences between those of the circumstances which appear to us to be pertinent. The proposition is now rather psychological than metaphysical. It would be impossible, with any evidentiary basis, to strengthen the expression ‘some considerable proportion’; and in other respects the statement is vague enough. Still, there is sufficient truth in it, perhaps, to warrant the presumptive adoption of hypotheses, provided this adoption merely means that they are taken as sufficiently reasonable to justify some expense in experimentation to test their truth by induction; but it gives no warrant at all to induction itself. For, in the first place, induction needs no such dubious support, since it is mathematically certain that the general character of a limited experience will, as that experience is prolonged, approximate to the character of what will be true in the long run, if anything is true in the long run. Now all that induction infers is what would be found true in the usual course of experience, if it were indefinitely prolonged. Since the method of induction must generally approximate to that truth, that is a sufficient justification for the use of that method, although no definite probability attaches to the inductive conclusion. In the second place, the law, as now formulated, neither helps nor hinders the validity of induction proper; for induction proper consists in judging of the relative frequency of a character among all the individuals of a class by the relative frequency of that character among the individuals of a random sample of that class. Now the law, as thus formulated, may tend to make our hypothesis approximately true; but that advantage has been gained before the operation of induction, which merely tests the hypothesis, begins. This inductive operation is just as valid when the hypothesis is bad as when it is good, when the character dealt with is trivial as when it is interesting. The ratio which induction ascertains may be nearer ½, and more remote from 1 or 0, when the characters are uninteresting; and in that case a larger number of instances will usually be requisite for obtaining the ratio with any given degree of precision (for if the ratio is really 1 or 0, it will be almost a miracle if in the sample it is far from that ratio, although this will not be impossible, if the whole class is infinite), but the essential validity of the process of induction remains unaffected by that circumstance.
What is usually meant by the uniformity of nature probably is that in proportion as the circumstances are alike or unlike, so are any phenomena connected with them alike or unlike. It may be asked to what degree nature is uniform in that sense. The only tenable answer is that it is as little uniform as it possibly could be imagined to be; for were any considerable proportion of existing uniformities, or laws, of nature destroyed, others would necessarily thereby result.
In fact, the great characteristic of nature is its diversity. For every uniformity known, there would be no difficulty in pointing out thousands of non-uniformities; but the diversities are usually of small use to us, and attract the attention of poets mainly, while the uniformities are the very staff of life. Hence, the higher and wider are our desires the greater will be the general impression of uniformity produced upon us by the contemplation of nature as it interests us.
(4) There are senses in which nature may not irrationally be held to be uniform; but opinions differ very widely as to the extent and nature of this uniformity. The chief of these are as follows:—
(a) The majority of physicists, at least of the older generation, hold, with regard to the physical universe, that its elements are masses, their positions, and the variations of these positions with time. It is believed that every motion exactly obeys certain laws of attraction and repulsion; and there is no other kind of law, except that each atom or corpuscle is a centre of energy arranged in equipotential surfaces about it, which follow a regular law; and that this is a permanency. But the equations of motion are differential equations of the second order, involving, therefore, two arbitrary constants for each moving atom or corpuscle, and there is no uniformity connected with these constants. At least, no such uniformity is, with the least probability, discoverable. As for the distribution of potential about an atom or corpuscle, it is regular; but there is no ulterior reason for that regularity, or, at least, none is probably discoverable. What is absolutely beyond discovery, whether direct and specific or indirect and general, may be considered to be non-existent.
From this usual and in some sense standard opinion there are many divergences in both directions. First, in the direction of greater uniformity.
(b) Some hold that there is some exact uniformity in the arbitrary constants of the motion of the atoms, so that, for example, perhaps at some initial instant they all had some symmetrical or regular arrangement, like a pack of cards unshuffled; and that the velocities at that instant were regular also. But this regularity being of a purely aesthetic or formal kind, and the laws of motion equally formal and unrelated to any purpose, it follows that all kinds of arrangements will be produced, ungoverned by any uniformity, but mere effects of chance. Three stars may, for example, at some instant form an equilateral triangle; but there would be no particular reason for this: it would be merely a casual coincidence.
(c) Others go further and maintain that the constants of position and velocity are subject to a law not merely formal, but are governed by final causes in such a way that there is no arrangement or coincidence whatever which was not specially intended by the Creator. To this theory, such words as pro-vidence and fore-knowledge are ill adapted; because the two constants which each atom or corpuscle has, remain constant throughout all time, and ought not to be considered as having been fixed at any particular epoch. The very idea is that the arrangement is determined by what would be the result of different arrangements at each period of time. If, for example, a given prayer effects rain, it must be supposed that, in view of that prayer, and as its consequence, the different atoms had the appropriate constants; but that these were not given to the atoms at any particular epoch, being permanent values. Any intentional action on the part of a free agent is to be explained in the same way. If an agent is to be supposed really free, it is difficult to see what other physical explanation is compatible with the exactitude of law. This seems to be substantially the notion of most of those who have supported free-will.
On the other hand, many philosophers suppose a less degree of uniformity in nature than is supposed in opinion (a). Of these the following have come to the present writer's notice as being actually defended.
(d) Some suppose that while law is absolute, yet there are constantly arising cases analogous to unstable equilibrium in which, owing to a passage of a velocity through infinity or otherwise, the law does not determine what the motion shall be. Thus if one Boscovichian point attracts another inversely as the square of the distance, and they move in one straight line, then when they come together they may move through one another, or move backwards on the same line, or may separate along any other line, without violating the differential equation. Such ‘singularities,’ as the mathematicians say, are theoretically possible; and may be supposed to occur very often. But to suppose that free action becomes possible in such a way is very illogical. In the first place, it supposes a direct interaction between ‘mind’ and matter; infinitesimal, no doubt, but none the less real. Why not better suppose a slight but finite action of this kind, and so avoid the following objections? Namely, in the second place, this is to put faith, not scientific credence, in the inductive laws of matter infinitely beyond what induction can ever warrant. We know very well that mind, in some sense, acts on matter, and matter on mind: the question is how. It is not in speculations of this fanciful kind that the true answer is likely to be found. In the third place, although this speculation wanders so far beyond all present knowledge, it nevertheless comes into conflict with a legitimate induction, namely, the supposition of any real ‘singularity’ or breach of continuity in nature is in as distinct conflict with all our knowledge as is a miracle.
(e) Sundry far less tenable hypotheses of lacunae between inviolable laws have often been proposed. One opinion frequently met with is that the law of energy does not prescribe the direction of velocity, but only its amount; so that the mind may cause atoms to ‘swerve,’ in regular Lucretian fashion. This singular notion has even been embraced by mathematicians, who are thinking of a projectile shot into a curved tube, or other case of an equation of condition. Of course, if mind can construct absolute constraints, it can much easier exert force that is finite. Other writers suppose lacunae, without telling us of what particular description they are; they seem to think law is absolute as far as it goes, but that its jurisdiction is limited.
(f) Much more philosophical and less logically objectionable is the notion of St. Augustine and others (it is near to the opinion of Aristotle) that the only fundamental kind of causation is the action of final causes, and that efficient causation is, in all cases, secondary. Accordingly, when a miracle occurs there is no violation of the real cursus naturae, but only of the apparent course of things.
(g) The hypothesis suggested by the present writer is that all laws are results of evolution; that underlying all other laws is the only tendency which can grow by its own virtue, the tendency of all things to take habits. Now since this same tendency is the one sole fundamental law of mind, it follows that the physical evolution works towards ends in the same way that mental action works towards ends, and thus in one aspect of the matter it would be perfectly true to say that final causation is alone primary. Yet, on the other hand, the law of habit is a simple formal law, a law of efficient causation; so that either way of regarding the matter is equally true, although the former is more fully intelligent. Meantime, if law is a result of evolution, which is a process lasting through all time, it follows that no law is absolute. That is, we must suppose that the phenomena themselves involve departures from law analogous to errors of observation. But the writer has not supposed that this phenomenon had any connection with free-will. In so far as evolution follows a law, the law of habit, instead of being a movement from homogeneity to heterogeneity, is growth from difformity to uniformity. But the chance divergences from law are perpetually acting to increase the variety of the world, and are checked by a sort of natural selection and otherwise (for the writer does not think the selective principle sufficient), so that the general result may be described as ‘organized heterogeneity,’ or, better, rationalized variety. In view of the principle of continuity, the supreme guide in framing philosophical hypotheses, we must, under this theory, regard matter as mind whose habits have become fixed so as to lose the powers of forming them and losing them, while mind is to be regarded as a chemical genus of extreme complexity and instability. It has acquired in a remarkable degree a habit of taking and laying aside habits. The fundamental divergences from law must here be most extraordinarily high, although probably very far indeed from attaining any directly observable magnitude. But their effect is to cause the laws of mind to be themselves of so fluid a character as to simulate divergences from law. All this, according to the writer, constitutes a hypothesis capable of being tested by experiment.
Literature: Besides most treatises on LOGIC (q.v., especially inductive) see Renouvier and Prat, La nouvelle Monadologie (1899). (C.S.P.) [726-31; CP 6.98-101]
Unity (and Plurality) [Lat. unitas, oneness]: Ger. Einheit (and Mehrheit); Fr. unité (and pluralité); Ital. unità (and pluralità). Formally, unity means whatever exists, or is considered, as a single, indivisible reality, and by whose repetition composite beings, or through whose agency derived beings, exist. (J.D.)
(1) A universally accepted understanding as to the formation of Latin words would require unity to mean that which is essential to the number one.
If we consider the number one, irrespective of the possibility of two, three, &c., it involves no idea of number (and therefore not of totality or collection), nor even any idea of relation. The idea would, therefore, be found in a pure state only in an immediate consciousness which should make no distinction of any kind, whether between subject and object, or of the parts of the object. But the term is never used in this sense, unless with an accompanying explanation.
(2) The oneness element of experience which involves a positive assignment of the number one, and which must be originally one, and not a total.
Much may be said for the opinion that we are thus brought to the event of acting and being acted upon; for that must be one, and is the only element of experience whose essential peculiarity is entirely lost in any generalization of it. The negative oneness of immediate consciousness—as, for example, it appears in the idea of any particular colour—does not resist generalization, the idea of redness in general having the same sort of unity as that of the scarlet of mercuric iodide or the colour of aniline red (magenta). But the moment I pass from the idea of a particular item of my experience, such as seeing a boat with a couple of men going over Niagara, to the slightest generalization of it, such as that of the memory of seeing the event, or the general conception of going over Niagara, the positive oneness entirely disappears.
Nevertheless, the word unity is seldom applied to this sort of oneness, which goes by the name of individuality. There is no individuality in a quality of immediate consciousness such as magenta or solferino, because there is no setting of object over against subject, which is requisite before oneness can be positively assigned to an idea (positive oneness thus involving duality); but neither is there any generality in the immediate consciousness, as long as it remains nothing more than what it first was. The purest oneness does not involve the least reference to plurality, and is therefore not positively opposed to generalization, and is not destroyed when generalization takes place. But positive and insistent oneness necessarily involves, or rather springs out of, the idea of duality, and distinctly denies it; so that generalization destroys it; it is the otherness of otherness, the negation of negation.
(3) The idea which the word unity is usually employed in philosophy to express is that of a general (in the most general sense) in its relation to particulars, which would be much more accurately called ‘totality.’
Unity is thus used, not to express pure oneness, nor yet positive oneness, but to express the negation of multitude in the object to which it is attributed. Thus it involves a distinct reference to the possibility, not of duality merely, as positive unity does, but of plurality (in the sense of more than two). The first unity might be named simplicity or firstness; the second is very appropriately termed individuality; the third, which is nearly what Kant terms synthetical unity, ought to have some better designation than totality or universality.
Unity in certain old books (as in the Institutiones Metaphysicae of Burgersdicius, 1647) is divided into singular and universal unity, the former belonging to singulars, the latter to universals. Singular unity is either material (or numerical) or formal. Material unity is defined as that which belongs to the singulars in so far as they are considered as units with individualizing differences; which is an awkward attempt to define individuality. Formal unity is ‘the unity which belongs to singulars abstractedly from their individualizing differences.’ These definitions depend upon a particular theory of individuation. Universal unity is distinguished from communicability, which is the reference to the plurality of singulars; and these two elements together make up universality. Numerical unity implies repugnance to multiplication; formal unity, indifference to multiplication; universal unity, non-repugnance to multiplication. The nature of the fundamentum universalitatis distinguishes the mediaeval realist from the nominalist. The nominalists generally do not admit that there is any similarity in things apart from the mind; but they may admit that this exists, provided they deny that it constitutes any unity among the things apart from the mind. They cannot admit the latter and remain consistent nominalists. Thus, a nominalist may admit that there is in the events themselves an agreement consisting in the uniformity with which all stones dropped from the hand fall to the ground; but if he admits that there is anything at all, except the mere fact that they happen to do so, that should in any sense determine the different stones to fall every time they are dropped, he ceases to be a good nominalist and becomes a mediaeval realist. Unity is further divided (by Burgersdicius, whom we continue to follow) into unity of simplicity and unity of composition. Simplicity is said to be unity devoid of all multitude; composition is the union of a plurality of things. This definition of simplicity is confessedly defective in representing this mode of unity as having a reference to multitude. Composition is divided into real, rational, and modal. Real composition is the union of distinct entities in the real thing itself. It is either actual or potential. Actual composition is either per compositionem, as when water and alcohol are mixed, or per aggregationem (as in an army). Potential composition is when one thing is united in potentia to another. It is either per informationem or per inhaerentiam; a distinction peculiar to a certain kind of Aristotelianism. Rational composition is either of things which differ by reason alone, or of things brought together in one concept; it includes, firstly, genera, species, &c.; secondly, equality, similitude, &c.; thirdly, agreement in effects, external causes, &c. Modal composition is composition from a thing and a mode. Most of the above distinctions go back to Scotus, and a few are still earlier.
Unity is divided by Kant into analytical and synthetical. He never defines or explains these terms; but if we remember that, in his use of words, multiplicity of elements is essential to unity, it is easy to see that what he means by analytical unity is the unity of that which is given in its combined state and is analysed by ordinary reflection. Thus we perceive a fact; and in order to express or think it, we analyse it, and the relation of the percept to the elements resulting from this analysis is very inappropriately called analytical unity. But when in the formation of the percept different sense impressions are put together, so that ordinary thought cannot proceed from whole to parts, but an operation more or less subconscious is supposed to manufacture the whole out of the parts, the relation of the whole to the parts is called synthetical unity. Three kinds of transcendental synthesis are recognized in the first edition of the Krit. d. reinen Vernunft, each resulting in a synthetical unity: they are the synthesis of apprehension in the intuition, which produces one representation; the synthesis of reproduction in the imagination; and the synthesis of recognition in the concept, which gives the unity of the rule. The transcendental unity of apperception is the unity which belongs to all my cognitions arising from a correlative unity of consciousness. It is transcendental, objective, and original. Besides these modes of transcendental unity, Kant recognizes other kinds of synthetical unity, some of which are empirical and contingent. There are also different modes of rational unity, some speculative, others moral.
That which the Scholastics meant by transcendental unity was unity in the sense in which it is said Quodlibet ens est unum, that is, is self-consistent.
We must not forget the three dramatic unities of time, place, and action, requiring the events represented to be included in one day, in one scene, and all to relate to one plot. Unity of action is set forth by Aristotle (Poetics, chaps. viii, ix, xviii). Unity of time is mentioned by him. That is, the action of a tragedy should, when convenient, be compressed into one day (Poetics, chap. v). The unity of place was remarked by French critics to have been observed by the Greek tragedians.
A unity in mathematics is a quantity which multiplied by any other gives that other. There can thus be but one unity in an algebra, although there may be many units. (C.S.P.) [734-6; concluding part of the article (p. 736, by J.D.) omitted here.]
Universal (and Universality) [Lat. universalis, pertaining to all]: Ger. allgemein; Fr. universel; Ital. universale. (1) This word was used in the middle ages where we should now use the word GENERAL (q.v.). Another synonym was praedicabile: ‘Praedicabile est quod aptum natum est praedicari de pluribus,’ says Petrus Hispanus. Albertus Magnus says, ‘Universale est quod cum sit in uno aptum natum est esse in pluribus.’ Burgersdicius, literally translating from Aristotle, says, ‘Universale (το καθ’ ὁλου) appello, quod de pluribus suapte natura praedicari aptum est,’ i.e., ὁ ἐπι πλειονων πεφυκε κατηγορεισθαι. When the Scholastics talk of universals, they merely mean general terms (which are said to be simple universals), with the exception here following.
(2) The five terms of second intention, or more accurately the five classes of predicates, genus, species, difference, property, accident, were in the middle ages (as they still are) called ‘the predicables.’ But since predicable also means fit to be a predicate, in which sense it is almost an exact synonym of universal in the first sense, the five predicables came to be often referred to as ‘the universals.’
(3) Predicated, or asserted, in a proposition de omni; said to be true, without exception, whatever there may be of which the subject term is predicable. See QUANTITY (in logic).
Thus ‘any phoenix rises from its ashes’ is a universal proposition. This is called the complex sense of universal. The subject must be taken in the distributive sense and not in the collective sense. Thus, ‘All man is all redeemed,’ which is Hamilton's ‘toti-total proposition,’ is not a universal proposition, or assertion de omni, in the sense defined by Aristotle in the dictum de omni; for it means that the collection of men is identical with the collection of the redeemed, and not that each man without exception is all redeemed. Leibnitz rightly insists that a universal proposition does not assert, or imply, the existence of its subject. The first reason for this is that it accords with the definition, that is, the dictum de omni, which is that that is asserted universally of a subject which is said to be predicable of whatever that subject may be predicable. For this may be done without asserting that the subject is predicable of anything in the universe. The second reason is that the term universal proposition is a term of formal logic. Now the principal, or at least the most essential, business of formal logic is so to formulate direct syllogism as not to represent it as requiring more or less than it really does. Now the major premiss of a direct syllogism must be universal, but need not imply the existence of anything of which the subject should be predicable. Hence a form of universal proposition not asserting the existence of the subject is indispensable. Now that no second kind of universal proposition is needed will presently appear. The third reason is that it is necessary that formal logic should be provided with a form of proposition precisely denying every proposition coming under each of its simple forms. Now, if a universal proposition asserting the existence of its subject is regarded as a simple form of proposition—as, for example, ‘There are inhabitants of Mars and every one of them without exception has red hair’—its precise denial would be a particular proposition not asserting the existence of the subject, which would be a most singular form, hardly ever wanted, and manifestly complex, such as, ‘Either there is no inhabitant of Mars, or if there be, there is one at least who has not red hair.’ It is obviously far better to make the simple particular proposition assert the existence of its subject, ‘There is an inhabitant of Mars who has red hair,’ when the universal form will not make the same assertion, or imply it: ‘Whatever inhabitants of Mars there may be must, without exception, have red hair.’ If every particular proposition asserts the existence of its subject, then an affirmative particular proposition implies the existence of its predicate also. It would be a contradiction in terms to say that a proposition asserted the existence of its predicate, since that of which a proposition asserts anything is its subject, not its predicate. But perhaps it is not quite accurate to say that the particular proposition asserts the existence of its subject. At any rate, this must not be understood as if, in such assertion, existence were a predicate not implied in a proposition which does not make this assertion (see Kant, Krit. d. reinen Vernunft, 1st ed., 599).
Every proposition refers to some index: universal propositions to the universe, through the environment common to speaker and auditor, which is an index of what the speaker is talking about. But the particular proposition asserts that, with sufficient means, in that universe would be found an object to which the subject term would be applicable, and to which further examination would prove that the image called up by the predicate was also applicable. That having been ascertained, it is an immediate inference, though not exactly asserted in the proposition, that there is some indicable object (that is, something existent) to which the predicate itself applies; so that the predicate also may be considered as referring to an index. Of course, it is perfectly legitimate, and in some aspects preferable, to formulate the particular proposition thus: ‘Something is, at once, an inhabitant of Mars and is red haired,’ and the universal proposition thus: ‘Everything that exists in the universe is, if an inhabitant of Mars, then also red haired.’ In this case, the universal proposition asserts nothing about existence; since it must already be well understood between speaker and auditor that the universe is there. The particular proposition in the new form asserts the existence of a vague something to which it pronounces ‘inhabitant of Mars’ and ‘red haired’ to be applicable.
The universal proposition must be understood as strictly excluding any single exception. It is thus distinguished from the proposition ‘The ratio of the number of A's to that of the A's that are B is as 1:1,’ not merely in being distributive in form instead of collective, but also in asserting much more. Thus the ratio of the multitude of all real numbers to those of them that are incommensurable is as 1:1, yet that does not prevent the commensurable numbers from existing, nor from being infinite in multitude. Were it proved that the ratio of frequency of all events to such of them as were due to natural causation was 1:1, that would be no argument whatever against the existence of miracles; although it might (or might not, according to circumstances) be an argument against explaining any given event as miraculous, if such a hypothesis can be called an explanation. Now induction may conclude that the ratio of frequency of a specific to a generic event is 1:1, in the same approximate sense in which all inductive conclusions are to be accepted. Indeed, the ratios 1:1 and 0:1 may be inductively concluded with stronger confidence in their accuracy than any other ratio can be so concluded. But under no circumstances whatsoever can induction establish the accuracy or approximate accuracy of a strictly universal proposition, or that any given series of phenomenal events is, properly speaking, general (and therefore represents a possibly infinite class), or is even approximately general. Such propositions, outside of mathematics (taking this word so as to include all definitions and deductions from them), must either be entirely unwarranted, or must derive their warrant from some other source than observation and experiment. It might conceivably be established by testimony, as, for example, by a promise by a possibly immortal being to act in a certain way upon every occasion of a certain description; and thus it would not need to be an a priori judgment. (C.S.P.) [737-8]
(4) The logical use (3) passes easily into the metaphysical. Provided the common attribute is regarded as important or essential, provided it is regarded as constituting a ‘natural’ genus or class, it expresses the essence of the thing under consideration—its permanent and abiding reality as distinct from transitory accidents. But since this essence is also what is common to a number of individuals, the class itself taken as an objective whole is regarded as a universal. When a predicate of this sort is applied to a subject, it expresses not merely an empirical, but a necessary, application to the whole of the subject-matter; the relationship ceases to be simply a quantitative one, and becomes qualitative or essential; e.g. ‘All swans are white’ would be a quantitative universal judgment, and so empirical. But ‘all events must have a cause’ is a qualitative universal—it is the ‘essence’ of an event to be caused. Now mediaeval thought was thus led to identify the universalia or generic notions with essences and with classes. Thus arose the discussion regarding the relation of universals to individual things (see REALISM, 1). Cf. ABSTRACT IDEAS.
(5) Aristotle had illustrated the common as the basis of a ‘natural’ class, by the common strain in various members of a family—those of common descent. This aspect of the term tends to identify the universal not merely with the static qualities or essence, but with the productive force—the generic is the generative—by which numerically distinct individuals are really connected with one another. This meaning presents a picture of what is meant by the objective reality of a universal. With modern science and the growth of the conception of force, causation, and the tendency to define (as in geometry) by reference to mode of production, this dynamic sense got the upper hand of the static. It is used in this sense in the school of Hegel to mean the general which, as function or activity, exists only in the specific differences to which it determines itself. (J.D.) [739]
(6) Kant, in sundry places (as in Logik by Jasche, § 21), draws a rather insignificant distinction between ‘generale’ or ‘gemeine’ Sätze and ‘universale’ or ‘allgemeine’ Sätze. The former are what are ordinarily called universal propositions. The latter are something more, apparently relating to any object whatsoever.
(7) Descartes, Leibnitz, Kant, and others appeal to the universality of certain truths as proving that they are not derived from observation, either directly or by legitimate probable inference. There is only one such passage in Descartes; and even Leibnitz, though he frequently alleges the necessity of certain truths (that is, their being propositions of necessary mode) against Locke's opinion, yet in only one place (the ‘Avant-Propos’ of the Nouveaux Essais) distinctly adds the criterion of universality. Descartes, Leibnitz, and Kant more or less explicitly state that that which they say cannot be derived from observation, or legitimate probable inference from observation, is a universal proposition in sense (3), that is, an assertion concerning every member of a general class without exception. Descartes (Letter xcix) argues that no legitimate inference can be made from external phenomena to the proposition that ‘Things equal to the same are equal to each other,’ since that would be to infer a ‘universal’ from a ‘particular.’ Leibnitz uses almost the same language: ‘D'où il nait une autre question, savoir, si toutes les vérités dépendent de l'expérience, c'est-à-dire de l'induction et des exemples, ou s'il y a un autre fondement.… Or, tous les exemples qui confirment une vérité générale, de quelque nombre qu'ils soient, ne suffisent pas pour établir la nécessité universelle de cette même vérité: car il ne suit pas que ce qui est arrivé arrivera toujours de même.’ Kant expresses himself still more unmistakably (Krit. d. reinen Vernunft, 2d ed., Einleitung, ii): ‘Erfahrung giebt niemals ihren Urtheilen wahre und strenge, sondern nur angenommene und comparative Allgemeinheit (durch Induction), so dass es eigentlich heissen muss: so viel wir bisher wahrgenommen haben, findet sich von dieser oder jener Regel keine Ausnahme. Wird also ein Urtheil in strenger Allgemeinheit gedacht, d. i. so, dass gar keine Ausnahme als möglich verstattet wird, so ist es nicht von der Erfahrung abgeleitet, sondern schlechterdings a priori gültig. Die empirische Allgemeinheit ist also nur eine willkührliche Steigerung der Gültigkeit, von der, welche in den meisten Fällen, zu der, die in allen gilt, wie z. B. in dem Satze: alle Körper sind schwer; wo dagegen strenge Allgemeinheit zu einem Urtheile wesentlich gehört, da zeigt diese auf einem besonderen Erkenntnissquell derselben, nämlich ein Vermögen des Erkenntnisses a priori. Nothwendigkeit und strenge Allgemeinheit sind also sichere Kennzeichen einer Erkenntniss a priori, und gehören auch unzertrennlich zu einander.’ But notwithstanding the fact that the whole logic of all these writers, especially Kant, requires the word universal to be understood in that sense, yet there are, in the works of all of them, some passages which lend a certain colour of excuse to the stupid blunder of some interpreters who teach that by necessity they mean the irresistible psychical force with which the proposition demands our assent, and that by universality they mean catholicity, i.e., the catholic acceptance of it semper, ubique, et ab omnibus. Descartes in particular, and Leibnitz in some measure, perhaps even Kant (though it would be very illogical for him to do so) did more or less attach weight to the irresistible apparent evidence, and to some degree to the catholic acceptance, of propositions as tending to persuade us of their truth; but not as criteria of their origin. It is, however, to be noticed that false interpreters of Kant have used the word universal in the sense of being accepted by all men—the sense of κοινος in the phrase κοιναι ἐννοιαι.
The words universal and universality enter into various technical phrases:— [these, ocupying pages 740-1, are omitted here, except the following which are included in CP 2.371:]
Natural universal: a natural sign predicable of a plurality of things, as smoke is a sign of fire. The nominalistic doctrine is that nothing out of the mind is universal in that sense. See Ockham, Logica, I. xiv ad fin.
Universal validity: according to some logicians is the validity of such reasonings as are ‘calculated to operate conviction on all reasonable minds’ (Hamilton, Lect. on Logic, xxvi). If he had omitted the word reasonable, and said ‘calculated to work conviction on all minds,’ this would not have proved they had any validity at all; for the validity of a reasoning depends upon whether it really will lead to the truth, and not upon whether it be believed that it will. Thus the word reasonable is the only pertinent word in the definition. But in fact there is no division of logical validity into universal and particular. (C.S.P., C.L.F.) [739-41]
Universe (the) [Lat. universum, combined, from unus, one, + vertere, to turn]: Ger. (das) Weltall; Fr. (l') univers, Ital. (l') universo. (1) The collection of all material things, το παν; the word universum occurs in this sense in Cicero.
‘Par l'espace,’ says Pascal (Pensées, i. 6), ‘l'univers me comprend et m'engloutit comme un point. Par la pensee, je le comprends.’ It is used by some writers to include the spiritual world; by others to include God.
(2) Universe (in logic) of discourse, of a proposition, &c. In every proposition the circumstances of its enunciation show that it refers to some collection of individuals or of possibilities, which cannot be adequately described, but can only be indicated as something familiar to both speaker and auditor. At one time it may be the physical universe of sense (1), at another it may be the imaginary ‘world’ of some play or novel, at another a range of possibilities.
The term was introduced by De Morgan in 1846 (Cambridge Philosophical Transactions, viii, 380) but De Morgan never showed that he fully comprehended it. It does not seem to be absolutely necessary in all cases that there should be an index proper outside the symbolic terms of the proposition to show what it is that is referred to; but in general there is such an index in the environment common to speaker and auditor. This De Morgan has not remarked; but what he has remarked has likewise its importance, namely, that for the purposes of logic it makes no difference whether the universe be wide or narrow. The idea of a limited logical universe was adopted by Boole and has been employed by all subsequent exact logicians. There is besides a universe of marks or characters, whenever marks are considered substantively, that is, as abstractions, as they commonly are in ordinary speech, even though the forms of language do not show it. Thus only, there comes to be a material difference between an affirmative and a negative proposition. For it will then alone be one thing to say that an object wants some character common to all men and another to say that it possesses every character common to all non-men. Only instead of giving three qualities it gives four, for the assertion may be that an object wants some character common to all non-men; a point made by ancient writers.
In 1882 O. C. Mitchell [sic; should be O. H. Mitchell?] extended the theory of the logical universe by the introduction of the idea of ‘dimension’ (see Logic (exact), ad fin.). (C.S.P., C.L.F.) [742, CP 2.536]
Vague (in logic) [Lat. vagus, rambling, indefinite]: Ger. unbestimmt ; Fr. vague; Ital. vago. Indeterminate in intention.
A proposition is vague when there are possible states of things concerning which it is intrinsically uncertain whether, had they been contemplated by the speaker, he would have regarded them as excluded or allowed by the proposition. By intrinsically uncertain we mean not uncertain in consequence of any ignorance of the interpreter, but because the speaker's habits of language were indeterminate; so that one day he would regard the proposition as excluding, another as admitting, those states of things. Yet this must be understood to have reference to what might be deduced from a perfect knowledge of his state of mind; for it is precisely because these questions never did, or did not frequently, present themselves that his habit remained indeterminate. (C.S.P.) [748]
Validity [Lat. validus, strong]: Ger. Gültigkeit; Fr. validité; Ital. validità. The possession by an argumentation or inference of that sort of efficiency in leading to the truth, which it professes to have; it is also said to be valid.
Every argument or inference professes to conform to a general method or type of reasoning, which method, it is held, has one kind of virtue or another in producing truth. In order to be valid the argument or inference must really pursue the method it professes to pursue, and furthermore, that method must have the kind of truth-producing virtue which it is supposed to have. For example, an induction may conform to the formula of induction; but it may be conceived, and often is conceived, that induction lends a probability to its conclusion. Now that is not the way in which induction leads to the truth. It lends no definite probability to its conclusion. It is nonsense to talk of the probability of a law, as if we could pick universes out of a grab-bag and find in what proportion of them the law held good. Therefore, such an induction is not valid; for it does not do what it professes to do, namely, to make its conclusion probable. But yet if it had only professed to do what induction does (namely, to commence a proceeding which must in the long run approximate to the truth), which is infinitely more to the purpose than what it professes, it would have been valid. Validity must not be confounded with strength. For an argument may be perfectly valid and yet excessively weak. I wish to know whether a given coin is so accurately made that it will turn up heads and tails in approximately equal proportions. I therefore pitch it five times and note the results, say three heads and two tails; and from this I conclude that the coin is approximately correct in its form. Now this is a valid induction; but it is contemptibly weak. All simple arguments about matters of fact are weak. The strength of an argument might be theoretically defined as the number of independent equal standard unit arguments upon the other side which would balance it. But since it is next to impossible to imagine independent arguments upon any question, or to compare them with accuracy, and since moreover the ‘other side’ is a vague expression, this definition only serves to convey a rough idea of what is meant by the strength of an argument. It is doubtful whether the idea of strength can be made less vague. But we may say that an induction from more instances is, other things being equal, stronger than an induction from fewer instances. Of probable deductions the more probable conclusion is the stronger. In the case of hypotheses adopted presumptively on probation, one of the very elements of their strength lies in the absence of any other hypothesis; so that the above definition of strength cannot be applied, even in imagination, without imagining the strength of the presumption to be considerably reduced. Perhaps we might conceive the strength, or urgency, of a hypothesis as measured by the amount of wealth, in time, thought, money, &c., that we ought to have at our disposal before it would be worth while to take up that hypothesis for examination. In that case it would be a quantity dependent upon many factors. Thus a strong instinctive inclination towards it must be allowed to be a favouring circumstance, and a disinclination an unfavourable one. Yet the fact that it would throw a great light upon many things, if it were established, would be in its favour; and the more surprising and unexpected it would be to find it true, the more light it would generally throw. The expense which the examination of it would involve must be one of the main factors of its urgency.
Returning to the matter of validity, an argument professing to be necessary is valid in case the premises could not under any hypothesis, not involving contradiction, be true, without the conclusion being also true. If this is so in fact, while the argument fails to make it evident, it is a bad argument rhetorically, and yet is valid; for it absolutely leads to the truth if the premises are true. It is thus possible for an argument to be valid and yet bad. Yet an argument ought not to be called bad because it does not elucidate steps with which readers may be assumed to be familiar. A probable deductive argument is valid, if the conclusions of precisely such arguments (from true premises) would be true, in the long run, in a proportion of times equal to the probability which this argument assigns to its conclusion; for that is all that is pretended. Thus, an argument that out of a certain set of sixty throws of a pair of dice about to be thrown, about ten will probably be doublets, is rendered valid by the fact that if a great number of just such arguments were made, the immense majority of the conclusions would be true, and indeed ten would be indefinitely near the actual average number in the long run. The validity of induction is entirely different; for it is by no means certain that the conclusion actually drawn in any given case would turn out true in the majority of cases where precisely such a method was followed; but what is certain is that, in the majority of cases, the method would lead to some conclusion that was true, and that in the individual case in hand, if there is any error in the conclusion, that error will get corrected by simply persisting in the employment of the same method. The validity of an inductive argument consists, then, in the fact that it pursues a method which, if duly persisted in, must, in the very nature of things, lead to a result indefinitely approximating to the truth in the long run. The validity of a presumptive adoption of a hypothesis for examination consists in this, that the hypothesis is selected according to a method which must ultimately lead to the discovery of the truth, so far as the truth is capable of being discovered, with an indefinite approximation to accuracy. (C.S.P., C.L.F.) [748-9]
Verification [Lat. verus, true, + facere, to make]: Ger. Bewährung, Bestätigung; Fr. vérification; Ital. verificazione. It is desirable to understand by a verifiable hypothesis one which presents an abundance of necessary consequences open to experimental tests, and which involves no more than is necessary to furnish a source of those consequences. The verification will not consist in searching the facts in order to find features that accord or disagree with the hypothesis. That is to no purpose whatsoever. The verification, on the contrary, must consist in basing upon the hypothesis predictions as to the results of experiments, especially those of such predictions as appear to be otherwise least likely to be true, and in instituting experiments in order to ascertain whether they will be true or not.
These experiments need not be experiments in the narrow and technical sense, involving considerable preparation. That preparation may be as simple as it may. The essential thing is that it shall not be known beforehand, otherwise than through conviction of the truth of the hypothesis, how these experiments will turn out. It does not need any long series of experiments, so long as every feature of the hypothesis is covered, to render it worthy of positive scientific credence. What is of much greater importance is that the experiments should be independent, that is, such that from the results of some, the result of no other should be capable of reasonable surmise, except through the hypothesis. But throughout the process of verification the exigencies of the economy of research should be carefully studied from the point of view of its abstract theory.
When, in 1839, Auguste Comte laid down the rule that no hypothesis ought to be entertained which was not capable of verification, it was far from receiving general acceptance. But this was chiefly because Comte did not make it clear, nor did he apparently understand, what verification consisted in. He seemed to think, and it was generally understood, that what was meant was that the hypothesis should contain no facts of a kind not open to direct observation. That position would leave the memory of the past as something not so much as to be entertained as plausible. (C.S.P.) [761-2]
Virtual [Lat. virtus, strength, from vir, a man]: Ger. virtuell; Fr. (1) virtuel; Ital. (1) virtuale. (1) A virtual X (where X is a common noun) is something, not an X, which has the efficiency (virtus) of an X.
This is the proper meaning of the word; but (2) it has been seriously confounded with ‘potential,’ which is almost its contrary. For the potential X is of the nature of X, but is without actual efficiency. A virtual velocity is something not a velocity, but a displacement; but equivalent to a velocity in the formula, ‘what is gained in velocity is lost in power.’
So virtual representation was the non-representation of the American colonies in the British Parliament, which was supposed to be replaced by something. So Milton asks whether the angels have virtual or immediate touch. So, too, the sun was said to be virtualiter on earth, that is, in its efficiency.
(3) Virtual is sometimes used to mean pertaining to virtue in the sense of an ethical habit.
Virtual knowledge: a term of Scotus defined by him (Opus Oxon., Pt. I. iii. 3) as follows : Quantum ad notitiam habitualem sive virtualem, primo expono quid intelligo per terminos. Habitualem notitiam voco, quando obiectum sic est praesens intellectui [i.e. to the thought] in ratione intelligibilis actu ut intellectus statim possit habere actum elicitum circa illud obiectuin. Voco virtualem, quando aliquid intelligitur in aliquo, ut pars intellecti primi, non autem ut primum intellectum sive ut totale terminans intellectionem. Hoc satis proprie vocatur intellectum virtualiter, quia est satis proximum intellecto in actu. Non enim posset esse actualius intellectum, nisi esset propria intellectione intellectum, quae esse ipsius primi, ut termini totalis.
Virtual difference: a term of the doctrine of formalitates set forth by Scotus, Opus Oxon., Pt. I. ii. 7. (C.S.P.) [763-4]
Whole (and Parts) [AS. hal, healthy; Gr. ὁλος, entire]: Ger. das Ganze; Fr. le tout; Ital. il tutto. The old definition is: ‘Totum est quod constat plurium rerum unione.’ Psychologically, whatever is treated as a single object, though capable of treatment as two or more objects (parts of the whole): by ‘treated’ meaning ‘thought of,’ ‘attended to,’ or otherwise ‘acted upon.’ (C.S.P.–J.M.B., G.F.S.)
We may say that a whole is an ens rationis whose being consists in the copulate being of certain other things, either not entia rationis or not so much so as the whole; so that a whole is analogous to a collection, which is, in fact, a special kind of whole. There can be no doubt that the word whole always brings before the mind the image of a collection, and that we interpret the word whole by analogy with collection. The idea of a collection is itself, however, by no means an easy one to analyze. It is an ens rationis, abstraction, or fictitious subject (but the adjective must be understood in a broad sense, to be considered below), which is individual, and by means of which we are enabled to transform universal propositions into singular propositions. Thus, the proposition ‘all men are mortal,’ with a new subject and new predicate, appears as ‘The collection of men is a collection of mortals’; just as, for other purposes, and by means of other abstractions, we transform the same proposition into ‘The character of mortality is possessed by every man’; and the members of the collection are regarded as less fictitious than the collection. It very often happens that an object given indirect perception as an individual is, on closer scrutiny, seen to be identifiable with a collection of parts. But it does not seem to be strictly accurate to say that the larger object of perception is identical with that abstraction, the collection of the smaller objects. It is rather something perceived which agrees in its relations with the abstraction so well that, for convenience, it is regarded as the same thing. No doubt the parts of a perceived object are virtually objects of consciousness in the first percept; but it is useless to try to extend logical relations to the sort of thought which antecedes the completion of the percept. By the time we conceive an object as a collection, we conceive that the first reality belongs to the members of the collection and that the collection itself is a mere intellectual aspect, or way of regarding these members, justified, in ordinary cases, by certain facts. We may, therefore, define a collection as a fictitious (thought) individual, whose being consists in the being of certain less fictitious individuals.
Many adjectives are used to distinguish different kinds of wholes. Certain of the phrases may be defined.
Actual whole: any whole which cannot exist without the existence of its parts. Usually identified with the Constitute whole. Monboddo's definition (Ancient Met., i. 479) is not quite accurate.
Collective whole, or aggregate whole: defined by Chauvin as ‘that which has material parts separate and accidentally thrown together into one, as an army,’ &c. But the example shows that organization does not disqualify a whole from being called collective, although the term totum per aggregationem will no longer be applied to it, in that case. In so far as a whole is collective, any other relation between its parts is put out of view.
Composite whole: a term of Burgersdicius, who (Inst. Met., I. xxii. § 7) defines it as ‘quod ex duabus partibus constat quarum una est in potentia ad alterum et altera vice versa actus est alterius.’ It includes the whole by information and the whole by inherence.
Comprehensive whole: a whole of logical comprehension.
Constituent whole: a whole which is essential to its parts. See UNIVERSAL.
Constitute whole: a whole whose parts are essential to it. See Actual whole (above).
Continuous whole: a continuum regarded as a whole. In order to define it, it would first be necessary to define continuity. Now we have, perhaps, not yet succeeded in analyzing the conception of continuity; for what the mathematicians call by that name, such as the relations of all real quantities capable of being designated to an indefinite degree of approximation by means of a whole number and a decimal, does not answer the requisites of the problem.
Copulative whole: a whole consisting of a sign which is essentially applicable to whatever certain signs, called its parts, are all applicable, but is essentially inapplicable to anything to which any one of these signs is inapplicable.
Definite whole: a whole constituted by genus and difference.
Definitive whole: see Definite whole (above).
Discrete whole: the same as a Collective whole (above).
Disjunctive whole: a whole consisting of a sign which is essentially applicable to whatever any one of certain signs, called its parts, is applicable, but is essentially inapplicable to anything to which none of these parts is applicable.
Dissimilar whole: same as Heterogeneous whole (below).
Essential whole: great confusion exists in the use of this very common expression. Aquinas (Summa Theol., Pt. I. lxxvi. 8) uses it in a broad sense which would make it about equivalent to Burgersdicius' composite whole, or perhaps broader. On the other hand, it is sometimes restricted to the whole per informationem, and this is perhaps the best settled use. But others make it include the physical and the metaphysical whole as its two species.
Extensive whole: a whole of logical extension, usually called a subjective or logical whole.
Formal whole: a comprehensive whole, especially of essential comprehension. See Actual whole (above).
Heterogeneous whole: a term of Aquinas; a whole whose parts are dissimilar from the whole.
Homogeneous whole: a term of Aquinas; a whole whose parts are similar to the whole, as the parts of a whole of water are.
Integral whole (a term in common use since Abélard's time): Blundevile (1599) says, ‘Whole integral is that which consisteth of integral parts, which though they cleave together, yet they are distinct and severall in number, as man's body, consisting of head, brest, belly, legs, &c.’ The usual definition is ‘quod habet partem extra partem,’ which restricts it to space. Burgersdicius, however, says that parts which differ in their ordinal places are partes extra partes.
Integrate whole: a pedantic variant of Integral whole (above).
Logical whole: same as Universal whole (below).
Mathematical whole: same as Integral whole (above).
Metaphysical whole: a whole in that respect in which a species is the whole of its genus and difference. See Formal whole (above).
Natural whole: a term proposed by Hamilton to replace Comprehensive or Metaphysical whole; as if that were not sufficiently provided with aliases under which to hide itself.
Negative whole: a unit regarded as a whole, as in the phrases ‘deus totus est ubique,’ and ‘anima est tota in toto corpore.’
[Objective Whole: a mental object apprehended as a single real thing.—J.M.B.]
Physical whole: a whole compounded of substance and accident; but some say of matter and form; and some that both come to the same thing. In the peripatetic view, however, substance is form, not matter.
Positive whole: a whole consisting of parts. See Negative whole (above).
Potential whole: same as Universal whole (below); so called because the genus does not actually, but only potentially, contain the species, &c.
Potestative whole: a term of Aquinas; equivalent to Potential whole (above).
Predicative whole: a whole of logical depth.
Quantitative whole: same as Integral whole (above).
Similar whole: see Homogeneous whole (above).
Subject whole: same as Subjective whole (below).
Subjective whole: a very venerable name for Universal whole (below).
Substantial whole: a whole of logical breadth.
Universal whole: see UNIVERSAL.
Whole by accident: such a whole as neither essentially belongs to the parts nor the parts to it.
Whole by aggregation or aggregative whole: same as Collective whole (above) in an exclusive sense.
Whole by information: a compound of act and power in the same kind, such as man, according to the Aristotelian theory of the soul.
Whole by inherence: same as Physical whole (above).
Whole by itself or per se: a whole which essentially belongs to its parts or its parts to it. (C.S.P.) [814-15, CP 6.381-3]
| Peirce page | gnoxic studies |